
{x|(wx)+b=+1} {x|(wx)+b=-1} 规范化的 最优分类面: X 》=-1 {x|(w·x)+b=0} margin 2/wll 解决方案:不妨把离分类面最近的样本的决策函数值归一化为1,即 强制: (w·4)-b21,若y,=1 等号成立的点 (w·4)-b≤-1,若y=-1 支持向量 亦即 y,[(wx)-b]≥1,i=1,…,1
规范化的 最优分类面:
X2 H1 1 ---.. 2 WX+ llwll H wx +b=0 W 0 ① b lwll

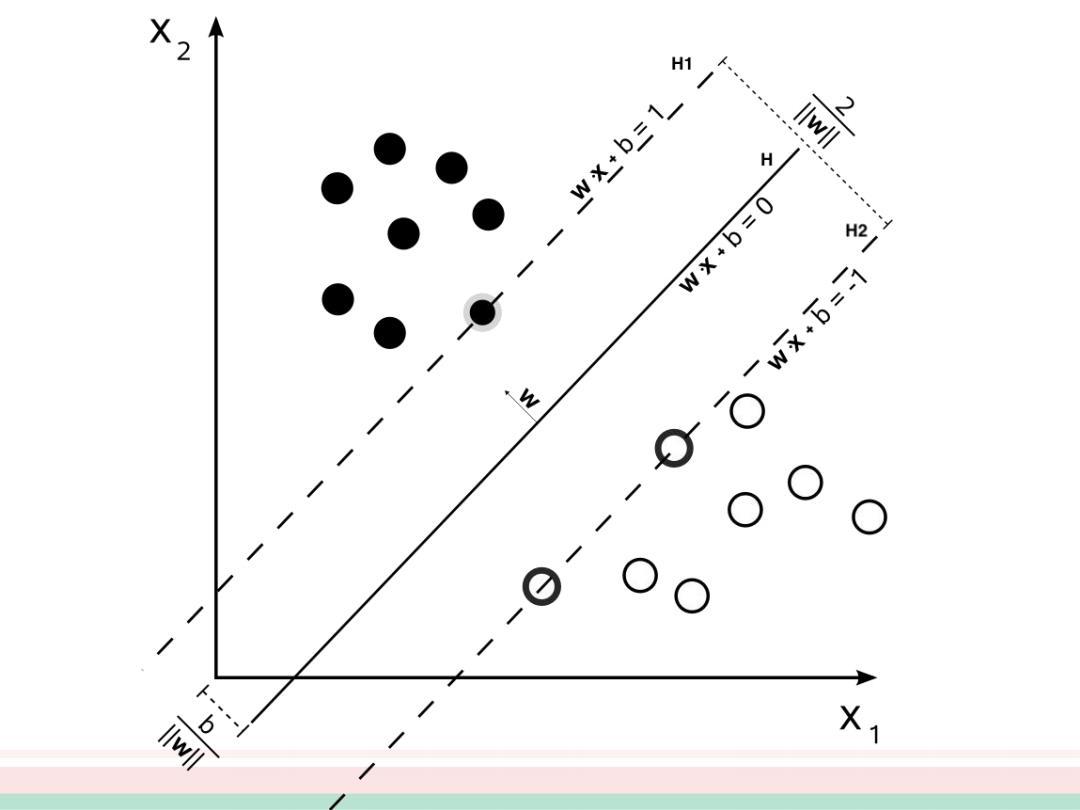
最优标准:分类间隔 >H2与H之间的间隔便是几何间隔。其中 >H1:<w,X>+b=1;H2:<WX>+b=-1; >几何间隔与样本的误分次数间的关系:误分次数<=(2R)2,其中δ 是样本集合到分类面的间隔,R=max‖il,i=1,,n; >所以问题转化成为求最大δ值。 H H. δ=2川w margin=2/w 图2线性可分情况下的最优分类线
最优标准:分类间隔 ØH2与H之间的间隔便是几何间隔。其中 Ø H1:<w,x>+b = 1;H2:<w,x>+b = -1; Ø几何间隔与样本的误分次数间的关系:误分次数 <= (2R/δ)^2,其中δ 是样本集合到分类面的间隔,R=max || xi ||,i=1,...,n; Ø所以问题转化成为求最大δ值。 δ = 2/||w||

最优标准:分类间隔 所谓最优分类面,就是在线性可分情 况下,要求分类线不但能将两类无错 误地分开,而且要使两类的分类空隙 最大。 间隔最大=> min 7 min 所有样本正确分类=> y,[(wx)+b]-1≥0,i=1,2,,n 等号成立的,点一支持向量(Support Vectors or SVs)
最优标准:分类间隔

采用拉格朗日Lagrangian)方法,问题成为: minmax w,b a L(w.b.c)-z(w-w)-Ecf[(w.x)+b]-B i=l s.t.h(wTxi+b)≥1,i=1,2,.,n 对偶问题 max min 4 w.b L(m,6四=m.w)-∑@iIw.x)+h1-1 s.t. (wci+b)≥1,i=1,2,.,n KKT条件 a,≥0 (wPc:+b)-1≥0 a(w2c:+b)-1=0
对偶问题 KKT条件