p=ETp的不存在例 ■ S={1,2,3},R= {<1,2>,<1,3>,<2,3>} ■E=(0,1,1),(0,0,1),(0,0,0) ET=(0,0,0),(1,0,0),(1,1,0) 不难看到,方程的成立 E" >p(1)=0→p(2)=0→p(3)=0 一 般来讲,p=Ep,意味着要求E「有特 征值1,这是很难得的
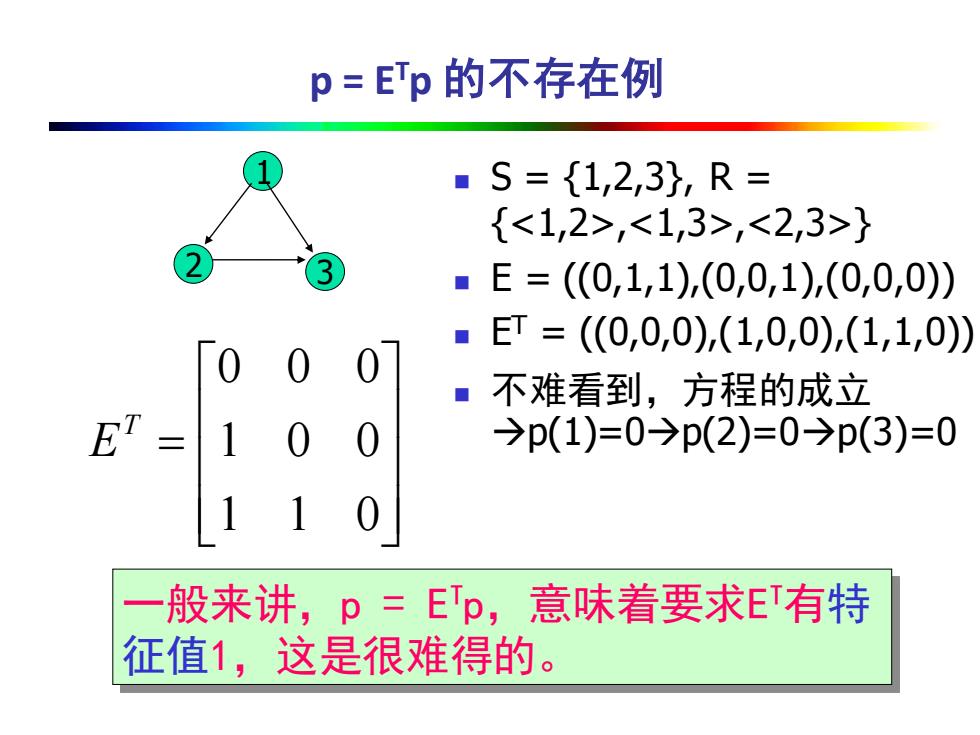
p = ETp 的不存在例 = 1 1 0 1 0 0 0 0 0 T E ◼ S = {1,2,3}, R = {<1,2>,<1,3>,<2,3>} ◼ E = ((0,1,1),(0,0,1),(0,0,0)) ◼ E T = ((0,0,0),(1,0,0),(1,1,0)) ◼ 不难看到,方程的成立 →p(1)=0→p(2)=0→p(3)=0 一般来讲,p = ETp,意味着要求E T有特 征值1,这是很难得的。 1 2 3
先前那4个点的例子也无解 p=ETp→(I-ET)p=O ■线性代数讲,此方程组有非0解,仅当行列式I一 ET|=0 但我们算得I一ET|=2
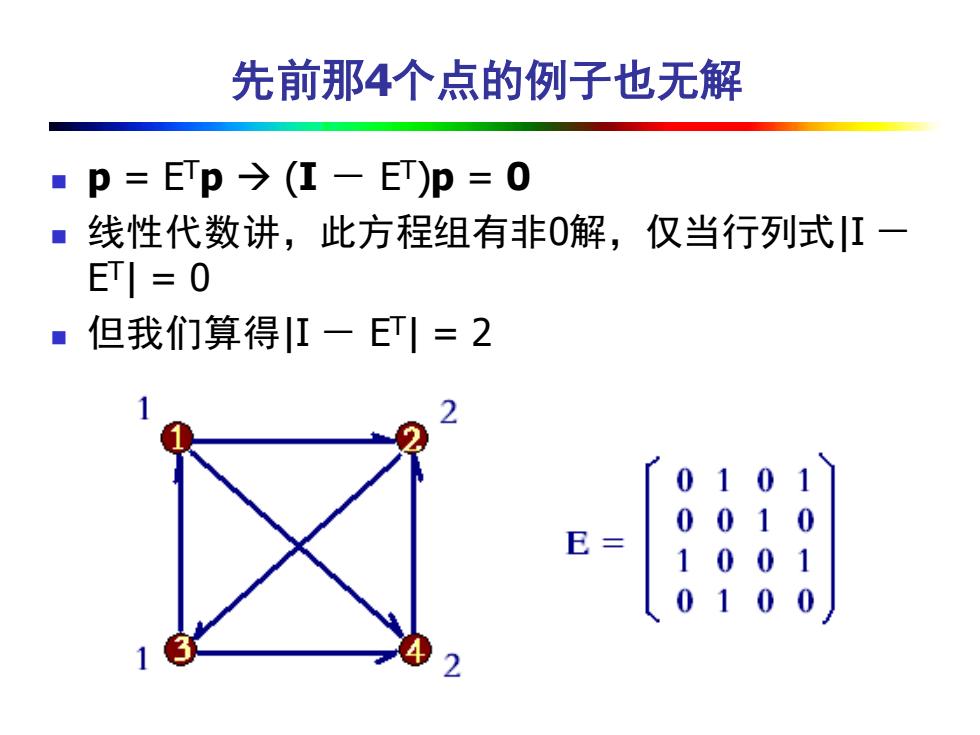
先前那4个点的例子也无解 ◼ p = ETp → (I - E T )p = 0 ◼ 线性代数讲,此方程组有非0解,仅当行列式|I - E T | = 0 ◼ 但我们算得|I - E T | = 2
即使有解,还有可能不唯一」 S={1,2,3},R={<1,2>,<2,3>,<3,1>} ■不难看出任何p(1)=p(2)=p(3)都是解 肉图 怎么办?
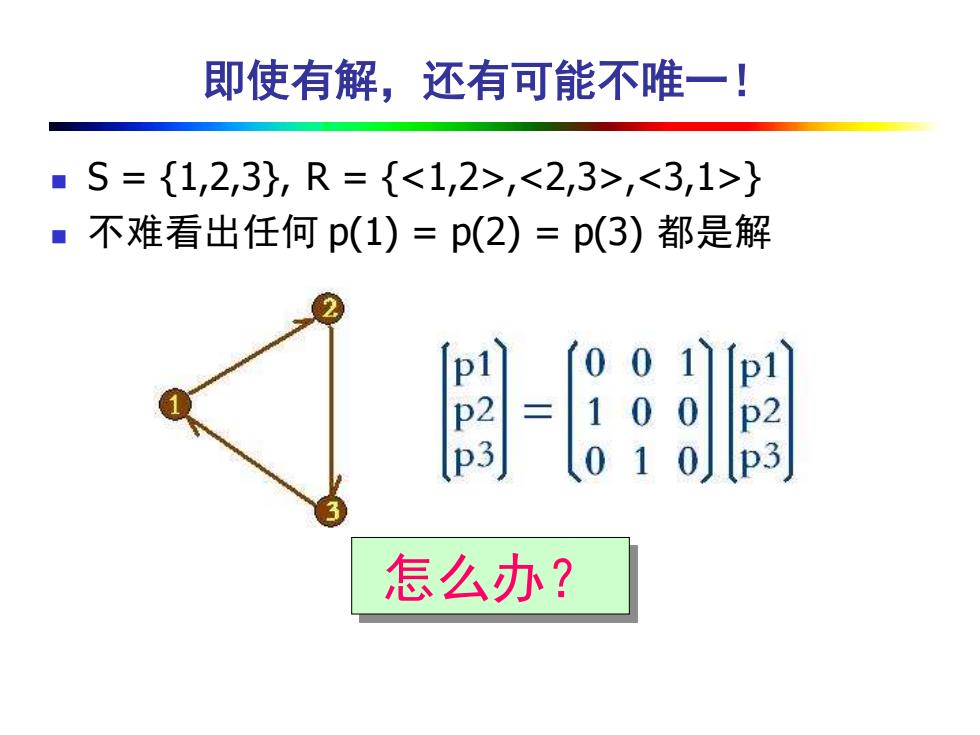
即使有解,还有可能不唯一! ◼ S = {1,2,3}, R = {<1,2>,<2,3>,<3,1>} ◼ 不难看出任何 p(1) = p(2) = p(3) 都是解 怎么办?
PageRank 对每一篇网页,得到一个独立于 查询词的相对“重要性”指标, 将这个指标和查询匹配情况结合 起来(以及其他因素),形成网 PageRankTM 页的排序。 “重要性” ·基本思想是前面讨论的“声望”模 型
PageRank ◼ 对每一篇网页,得到一个独立于 查询词的相对“重要性”指标, 将这个指标和查询匹配情况结合 起来(以及其他因素),形成网 页的排序。 ◼ “重要性” ◼ 基本思想是前面讨论的“声望”模 型

“Random Walker'"模型 ■设想有一个永不休止、在网上浏览网页的人,随机 选择一个链出的链接继续访问。我们问,在稳态情 况下(足够长时间后),他会正在看哪一篇网页呢? ■等价于:稳态情况下,每个网页V会有一个被访问 的概率,p(),它可以作为网页的重要程度的度量。 ■我们可以合理地设想:此时到达V的概率,依赖于 上一个时刻到达“链向”V的网页的概率,以及那 些网页中超链的个数
“Random Walker”模型 ◼ 设想有一个永不休止、在网上浏览网页的人,随机 选择一个链出的链接继续访问。我们问,在稳态情 况下(足够长时间后),他会正在看哪一篇网页呢? ◼ 等价于:稳态情况下,每个网页v会有一个被访问 的概率,p(v),它可以作为网页的重要程度的度量。 ◼ 我们可以合理地设想:此时到达v的概率,依赖于 上一个时刻到达“链向”v的网页的概率,以及那 些网页中超链的个数