递归函数举例 例2 Fibonacci数列 无穷数列1,1,2,3,5,8,13,21,34,55,…, 被称为Fibonacci数列。它可以递归地定义为: n=0 边界条件 、 F(n)={ n=1 F(n-1)+F(n-2)n>1 递归方程 第n个Fibonacci数可递归地计算如下: public static int fibonacci(int n) { if (n <1)return 1; return fibonacci(n-1)+fibonacci(n-2); 11 }
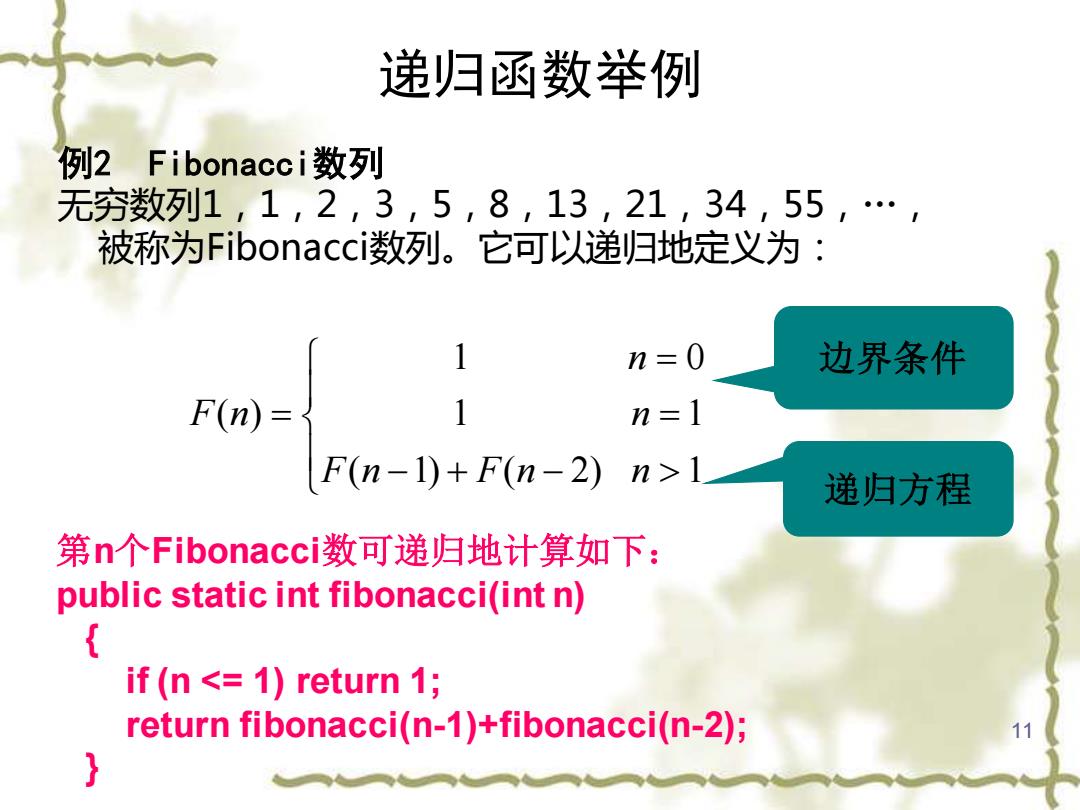
11 递归函数举例 例2 Fibonacci数列 无穷数列1,1,2,3,5,8,13,21,34,55,…, 被称为Fibonacci数列。它可以递归地定义为: 边界条件 递归方程 1 1 0 ( 1) ( 2) 1 1 ( ) = = − + − = n n n F n F n F n 第n个Fibonacci数可递归地计算如下: public static int fibonacci(int n) { if (n <= 1) return 1; return fibonacci(n-1)+fibonacci(n-2); }

递归函数举例 例3 Ackermani函数 当一个函数及它的一个变量是由函数自身定义时,称这个 函数是双递归函数。 Ackerman函数A(n,m)定义如下: A(1,0)=2 A(0,m=1 m≥0 A(n,0)=n+2 n≥2 A(n,m)=A(A(n-1,m),m-1)n,m=1 12
12 递归函数举例 例3 Ackerman函数 当一个函数及它的一个变量是由函数自身定义时,称这个 函数是双递归函数。 Ackerman函数A(n,m)定义如下: = − − = + = = , 1 2 0 ( , ) ( ( 1, ), 1) ( ,0) 2 (0, ) 1 (1,0) 2 n m n m A n m A A n m m A n n A m A

例3 Ackerman函数 前2例中的函数都可以找到相应的非递归方式定义: n!=1.2.3…(n-1)n n+l 但本例中的Ackerman函数却无法找到非递归的定义。 13
13 例3 Ackerman函数 前2例中的函数都可以找到相应的非递归方式定义: n!= 1 2 3(n −1) n − − + = +1 +1 2 1 5 2 1 5 5 1 ( ) n n F n 但本例中的Ackerman函数却无法找到非递归的定义

例3 Ackerman函数 ÷A(n,m)的自变量m的每一个值都定义了一个单变量函数: M=0时,A(n,0)=n+2 M=1时,A(n,1)=A(A(n-1,1),0)=A(n-1,1)+2,和 A(1,1)=2故A(n,1)=2*n M=2时,A(n,2)=A(A(n-1,2),1)=2A(n-1.2),和 A(1,2)=A(A(0,2),1)=A(1,1)=2,故An,2)=2n 2 M=3时,类似的可以推出 Z M=4时,A(n,4)的增长速度非常快,以至于没有适当的数 学式子来表示这一函数
14 例3 Ackerman函数 ❖ A(n,m)的自变量m的每一个值都定义了一个单变量函数: ❖ M=0时,A(n,0)=n+2 ❖ M=1时,A(n,1)=A(A(n-1,1),0)=A(n-1,1)+2,和 A(1,1)=2故A(n,1)=2*n ❖ M=2时,A(n,2)=A(A(n-1,2),1)=2A(n-1,2),和 A(1,2)=A(A(0,2),1)=A(1,1)=2,故A(n,2)= 2^n 。 ❖ M=3时,类似的可以推出 ❖ M=4时,A(n,4)的增长速度非常快,以至于没有适当的数 学式子来表示这一函数。 n 2 2 2 2

例3 Ackerman函数 定义单变量的Ackerman函数A(n)为, A(n)=A(n,n)。 定义其逆函数a(n)为:(n)=mink A(k)≥n}。即a(n)是使n≤A(k)成立的最小的 k值。 a()在复杂度分析中常遇到。对于通常所见 到的正整数n,有a(n)s4。但在理论上o(n) 没有上界,随着的增加,它以难以想象的慢 速度趋向正无穷大
15 例3 Ackerman函数 ❖ 定义单变量的Ackerman函数A(n)为, A(n)=A(n,n)。 ❖ 定义其逆函数α(n)为:α(n)=min{k| A(k)≥n}。即α(n)是使n≤A(k)成立的最小的 k值。 ❖ α(n)在复杂度分析中常遇到。对于通常所见 到的正整数n,有α(n)≤4。但在理论上α(n) 没有上界,随着n的增加,它以难以想象的慢 速度趋向正无穷大