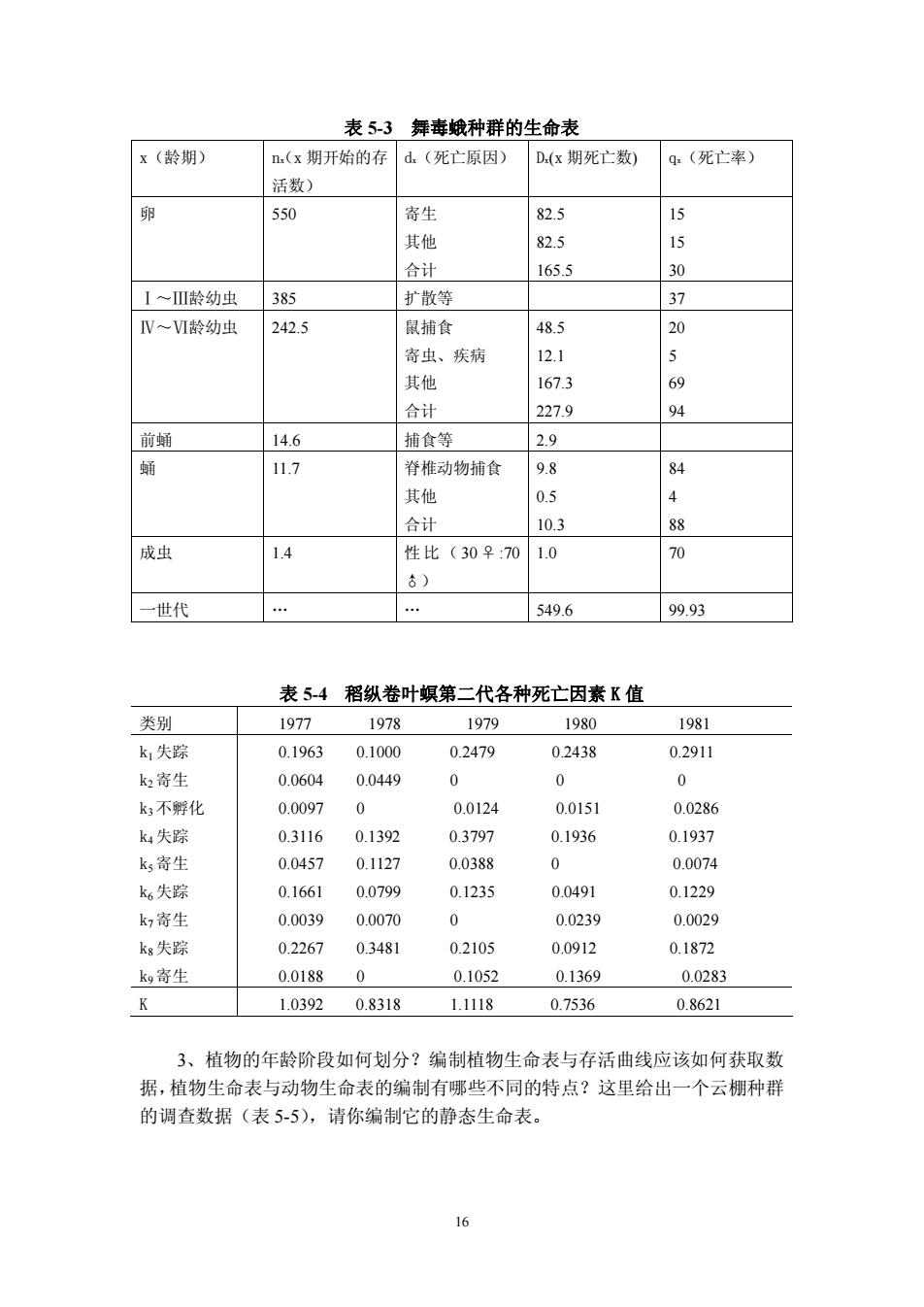
表53舞毒娥种群的生命表 x(龄期) n.(x期开始的存d.(死亡原因) D(x期死亡数) (死亡率) 活数) 550 寄生 82.5 其他 82.5 15 合计 165.5 30 I一川龄幼虫 385 扩撒等 37 V~I龄幼虫 242.5 鼠捕食 48.5 20 寄虫、疾病 12.1 5 其他 167.3 69 合计 227.9 94 前蛹 14.6 捕食等 2.9 117 脊推动物捕食 9.8 其他 0.5 4 合 10.3 88 成虫 1.4 性比(30♀:70 1.0 70 片) 一世代 549.6 99.93 表54稻纵卷叶螟第二代各种死亡因素K值 类别 1977 1978 1979 1980 1981 k,失踪 0.1963 0.1000 0.2479 0.2438 0.2911 k2寄生 0.0604 0.0449 0 0 k:不每化 0.0097 0 0.0124 0.0151 0.0286 k4失踪 0.3116 0.1392 0.3797 0.1936 0.1937 k,寄生 0.0457 0.1127 0.0388 0 0.0074 k6失踪 0.1661 0.0799 0.1235 0.0491 0.1229 k,寄生 0.0039 0.0070 0 0.0239 0.0029 k失踪 0.2267 0.3481 0.2105 0.0912 0.1872 k。客生 001880 0.1052 01369 00283 1.0392 0.8318 1.1118 0.7536 0.8621 3、植物的年龄阶段如何划分?编制植物生命表与存活曲线应该如何获取数 据,植物生命表与动物生命表的编制有哪些不同的特点?这里给出一个云棚种群 的调查数据(表5-5),请你编制它的静态生命表
16 表 53 舞毒蛾种群的生命表 x(龄期) n(x x 期开始的存 活数) dx(死亡原因) Dx(x 期死亡数) qx(死亡率) 卵 550 寄生 其他 合计 82.5 82.5 165.5 15 15 30 Ⅰ~Ⅲ龄幼虫 385 扩散等 37 Ⅳ~Ⅵ龄幼虫 242.5 鼠捕食 寄虫、疾病 其他 合计 48.5 12.1 167.3 227.9 20 5 69 94 前蛹 14.6 捕食等 2.9 蛹 11.7 脊椎动物捕食 其他 合计 9.8 0.5 10.3 84 4 88 成虫 1.4 性比(30♀:70 ♂) 1.0 70 一世代 . . 549.6 99.93 表 54 稻纵卷叶螟第二代各种死亡因素 K 值 类别 1977 1978 1979 1980 1981 k1失踪 k2寄生 k3不孵化 k4失踪 k5寄生 k6失踪 k7寄生 k8失踪 k9寄生 0.1963 0.1000 0.2479 0.2438 0.2911 0.0604 0.0449 0 0 0 0.0097 0 0.0124 0.0151 0.0286 0.3116 0.1392 0.3797 0.1936 0.1937 0.0457 0.1127 0.0388 0 0.0074 0.1661 0.0799 0.1235 0.0491 0.1229 0.0039 0.0070 0 0.0239 0.0029 0.2267 0.3481 0.2105 0.0912 0.1872 0.0188 0 0.1052 0.1369 0.0283 K 1.0392 0.8318 1.1118 0.7536 0.8621 3、植物的年龄阶段如何划分?编制植物生命表与存活曲线应该如何获取数 据, 植物生命表与动物生命表的编制有哪些不同的特点?这里给出一个云棚种群 的调查数据(表 55),请你编制它的静态生命表
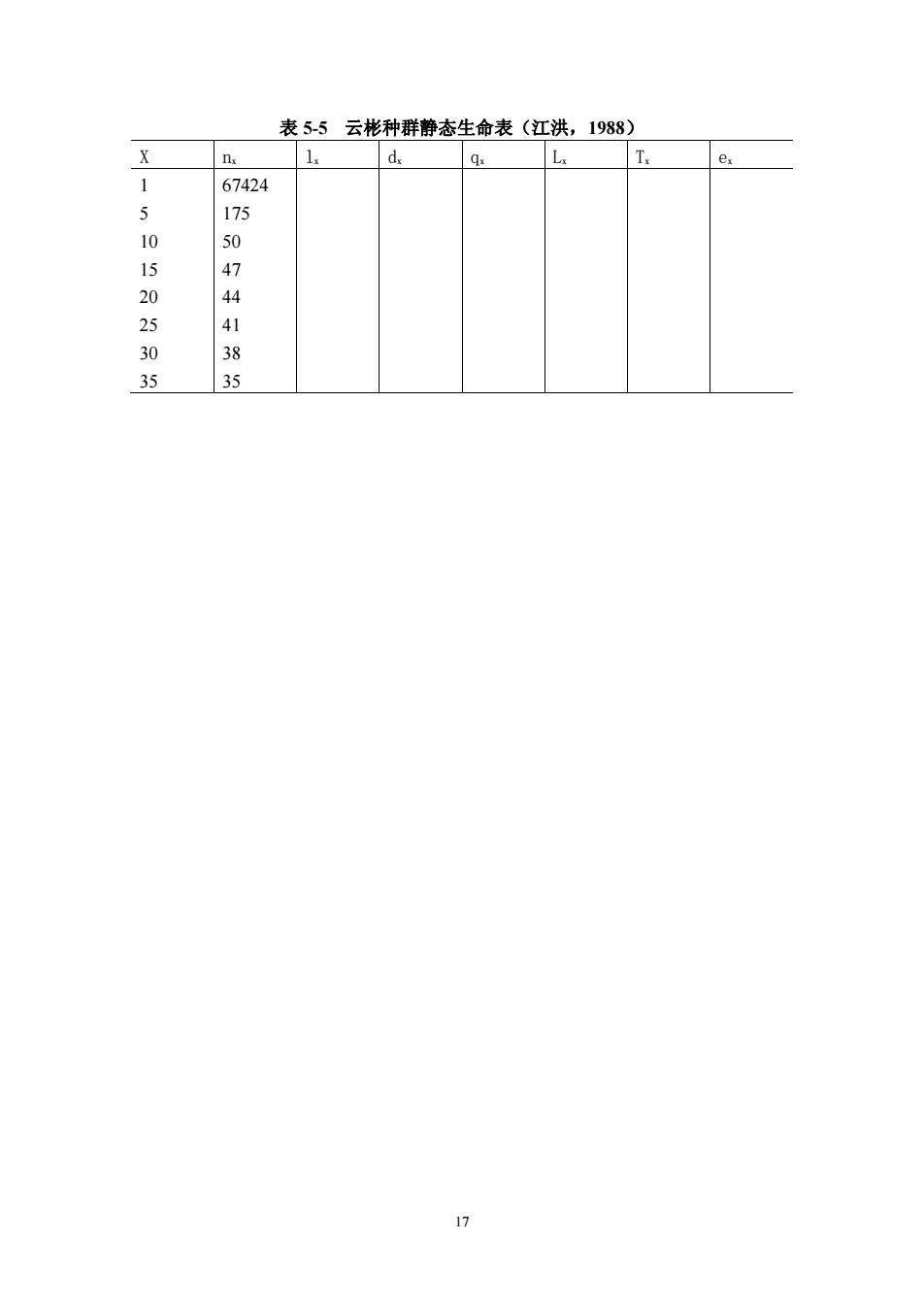
表55云彬种群静态生命表(江洪,1988) X n. 1. d e 67424 5 175 15 44 25 1 30 36 35
17 表 55 云彬种群静态生命表(江洪,1988) X nx lx dx qx Lx Tx ex 1 5 10 15 20 25 30 35 67424 175 50 47 44 41 38 35

实验六Lotka-一Volterra捕食者一猎物模型模拟 实验原理」 Lotka-一Volterra捕食者一猎物模型是20世纪20年代Lotka A.J.(1925)和 Volterra V.(1926)提出的描述种间关系的经典模型之一。该模型假设:1、除捕 食者存在外,猎物生活于理想环境中(其出生率和死亡率与密度无关)。2、捕食 者的环境同样是理想的,它的种群增长只受到可获得的猎物数量限制。 Lotka一Volterra捕食者一猎物系统的连续增长微分方程为: dN/dt=riN-CiNP (1) dP/dt=r2P+C2NP (2) 式中:N为猎物密度 为猎物的内禀增长率 C1是猎物与捕食者相遇被吃掉的儿率 P是捕食者密度 2是捕食者的内禀增长率 C2是捕食者攻击效率(捕食能力)的测度 方程(1)描述了猎物种群动态,倾向于rN的无限增长,但它要受捕食者 功能项CNP的制约 方程(2) 描述了捕食种群动态, 一方面受死亡的影响,另一方面捕食者数 量还要受与猎物密度有关的数值反应CNP的影响。 当模型在平衡时即:dN/d=dPdt=0时,则P=r/C,N=2C2。说明当捕食者 的数量为「C1时,猎物数量将稳定不变:大于rC时,猎物的数量会减少:小 于rC1,则猎物数量增加。同样猎物数量为2/C2时,捕食者数量也会恒定不变: 大于C2时,捕食者数量上升:反之则捕食者数量下降 Lotka-一Volterra捕食者- 猎物模型,揭示了这种捕食关系的两个种群数量 动态是彼此消长,往复震荡的变化规律。 [实验目的 在掌握Loka一otem捕食者一猎物模型的生态学意义与各参数意义的 实验仪器] windows98、2000或XP运行平台、Lotka-一olterra捕食者一猎物模型计 算机模拟运行软件。 方法与步骤 (一)参数的设置 1、N=0,r=0.1,C1=0.01:P=20,r2=0.1,C20.01: 2、N=20,r1=0.1,C1-0.01:P=0,2=0.1,C2=0.01: 3、N=20,r=0.1,C,=0.01:P=20,r=0.1,C,=0.01 4、N=5 01,C,-0.01:P=20,r2 0.1,C20.01: 5 固定 P和N,改变r或C, (二)结果分析 1、当捕食者p0时,猎物种群增长的变化规律? 2、当猎物N-0时,捕食者种群增长的变化规律?
18 实验六 Lotka—Volterra 捕食者—猎物模型模拟 [实验原理] Lotka—Volterra 捕食者—猎物模型是 20 世纪 20 年代 Lotka A.J.(1925)和 Volterra V.(1926)提出的描述种间关系的经典模型之一。该模型假设:1、除捕 食者存在外,猎物生活于理想环境中(其出生率和死亡率与密度无关)。2、捕食 者的环境同样是理想的,它的种群增长只受到可获得的猎物数量限制。 Lotka—Volterra 捕食者—猎物系统的连续增长微分方程为: dN/dt=r1NC1NP (1) dP/dt=r2P+C2NP (2) 式中:N 为猎物密度 r1 为猎物的内禀增长率 C1 是猎物与捕食者相遇被吃掉的儿率 P 是捕食者密度 r2 是捕食者的内禀增长率 C2 是捕食者攻击效率(捕食能力)的测度 方程(1)描述了猎物种群动态,倾向于 r1N 的无限增长,但它要受捕食者 功能项 C1NP 的制约。 方程(2)描述了捕食种群动态,一方面受死亡的影响,另一方面捕食者数 量还要受与猎物密度有关的数值反应 C2NP 的影响。 当模型在平衡时即:dN/dt=dP/dt=0 时,则 P=r1/C1 N=r2/C2。说明当捕食者 的数量为 r1/C1 时,猎物数量将稳定不变;大于 r1/C1 时,猎物的数量会减少;小 于 r1/C1,则猎物数量增加。同样猎物数量为 r2/C2 时,捕食者数量也会恒定不变; 大于 r2/C2 时,捕食者数量上升;反之则捕食者数量下降。 Lotka—Volterra 捕食者——猎物模型,揭示了这种捕食关系的两个种群数量 动态是彼此消长,往复震荡的变化规律。 [实验目的] 在掌握 Lotka—Volterra 捕食者——猎物模型的生态学意义与各参数意义的 基础上,通过改变相应参数值的大小,在计算机上模拟捕食者种群与猎物种群的 数量变化规律,从而加深对该模型的认识。 [实验仪器] windows98、2000 或 XP 运行平台、Lotka—Volterra 捕食者——猎物模型计 算机模拟运行软件。 [方法与步骤] (一)参数的设置 1、 N=0,r1=0.1,C1=0.01;P=20,r2=0.1,C2=0.01; 2、 N=20,r1=0.1,C1=0.01;P=0,r2=0.1,C2=0.01; 3、 N=20,r1=0.1,C1=0.01;P=20,r2=0.1,C2=0.01; 4、 N=5,r1=0.1,C1=0.01;P=20,r2=0.1,C2=0.01; 5、 固定 P 和 N,改变 r 或 C, (二)结果分析 1、 当捕食者 p=0 时,猎物种群增长的变化规律? 2、 当猎物 N=0 时,捕食者种群增长的变化规律?
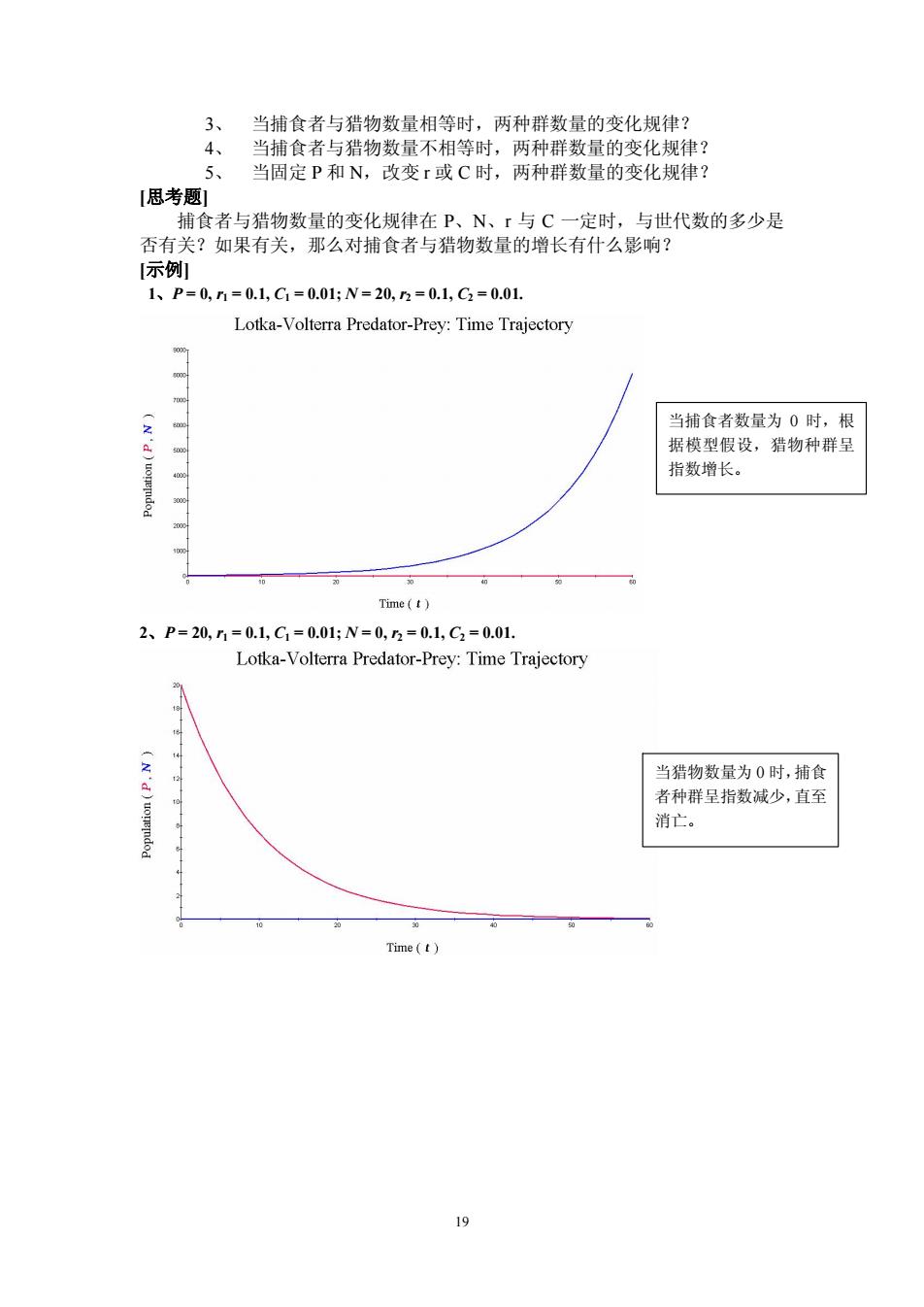
3、当捕食者与猎物数量相等时,两种群数量的变化规律? 4、 当捕食者与猎物数量不相等时,两种群数量的变化规律? 、 当固定P和N,改变r或C时,两种群数量的变化规律? [思考题 捕食者与猎物数量的变化规律在P、N、「与C一定时,与世代数的多少是 否有关?如果有关,那么对捕食者与猎物数量的增长有什么影响? 示例 1、P=0,n=0.1,C=0.01:N-20,n=0.1,G2=0.01 Lotka-Volterra Predator-Prey:Time Trajectory 当捕食者数量为0时,根 据模型假设,猎物种群呈 指数增长。 Time(t) 2、P=20,n=0.1,C1=0.01;N=0,5=0.1,C2=0.0L. Lotka-Volterra Predator-Prey:Time Trajectory 1 当猎物数量为0时,捕食 者种群呈指数减少,直至 消二。 Time(t)
19 3、 当捕食者与猎物数量相等时,两种群数量的变化规律? 4、 当捕食者与猎物数量不相等时,两种群数量的变化规律? 5、 当固定 P 和 N,改变 r 或 C 时,两种群数量的变化规律? [思考题] 捕食者与猎物数量的变化规律在 P、N、r 与 C 一定时,与世代数的多少是 否有关?如果有关,那么对捕食者与猎物数量的增长有什么影响? [示例] 1、P = 0, r1 = 0.1, C1 = 0.01; N = 20, r2 = 0.1, C2 = 0.01. 2、P = 20, r1 = 0.1, C1 = 0.01; N = 0, r2 = 0.1, C2 = 0.01. 当捕食者数量为 0 时,根 据模型假设,猎物种群呈 指数增长。 当猎物数量为 0 时, 捕食 者种群呈指数减少, 直至 消亡
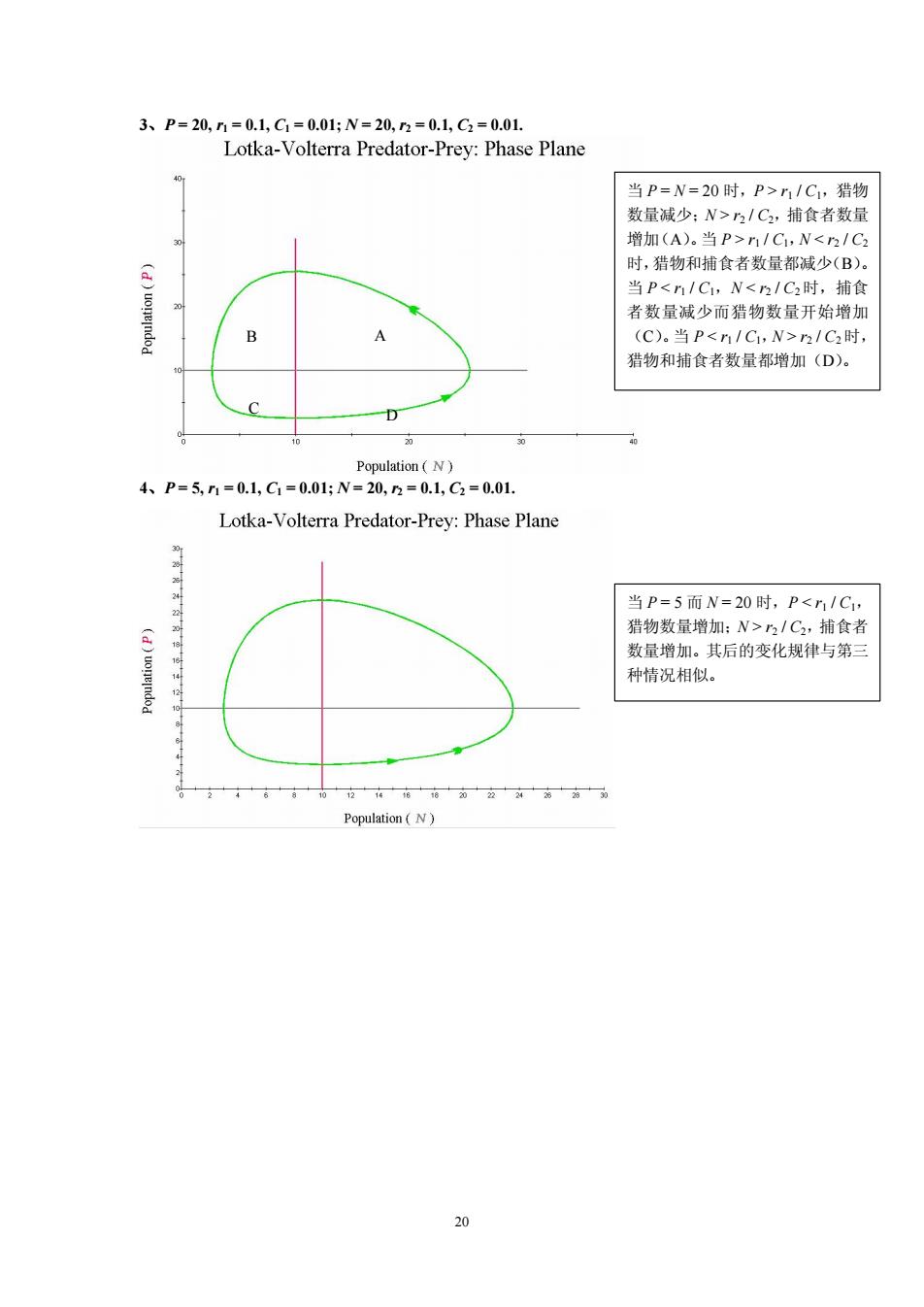
3、P=20,n=0.1,C1=0.01;N=203=0.l,C2=0.01. Lotka-Volterra Predator-Prey:Phase Plane 当P=N=20时,P>nIC,猎物 数量减少:N>21C2,捕食者数量 增加(A).当P>nG,N<n/C 时,猎物和捕食者数量都减少(B) 当P<n/C,N<n/C2时,捕食 者数量减少而猎物数量开始增加 (C)。当P<n/C,N>h1C2时, 猎物和捕食者数量都增加(D)。 Population(N)) 4、P=5,n=0.l,C1=0.01;N=20,n=0.L,C2=0.01. Lotka-Volterra Predator-Prey:Phase Plane 当P=5而N=20时,P<1/C, 猎物数最增加:N> 1C,捕食 数量增加。其后的变化规律与第 种情况相似 Population(N)
20 3、P = 20, r1 = 0.1, C1 = 0.01; N = 20, r2 = 0.1, C2 = 0.01. 4、P = 5, r1 = 0.1, C1 = 0.01; N = 20, r2 = 0.1, C2 = 0.01. 当 P = N = 20 时,P > r1 / C1,猎物 数量减少;N > r2 / C2,捕食者数量 增加 (A)。 当 P > r1 / C1,N < r2 / C2 时, 猎物和捕食者数量都减少 (B)。 当 P < r1 / C1,N < r2 / C2时,捕食 者数量减少而猎物数量开始增加 (C)。 当 P < r1 / C1,N > r2 / C2时, 猎物和捕食者数量都增加(D)。 当 P = 5 而 N = 20 时,P < r1 / C1, 猎物数量增加;N > r2 / C2,捕食者 数量增加。其后的变化规律与第三 种情况相似。 B A C D