
(三)逻辑斯谛方程的拟合 1、通过做图目测估计法、平均值法、三点法等方法,计算或估计K、 a的值 2、将每天的观测数据记录在自制的观测数据记录表格中。 (四)实验分组和讨论 1、实验分组 本实验可由学生分组进行,并可在不同的环境条件下进行对比实验。环境容 纳量也象其他生态特征一样,是随环境条件的不同而改 变的。因此逻辑斯谛增长 曲线对于某一种生物也不是固定不变的。如改变培养温度,将草履虫培养液放舀 在不同的培养温度下培养。对所得到的不同温度下的草履虫种群增长曲线,可以 让同学们来讨论环境条件的改变对草履虫实验种群增长的影响。 2、实验讨论 ①撰写实验报告,绘制草履虫实验种群的罗辑斯谛增长曲线 ②讨论实验中各种实验条件的不同可能给草履虫种群增长造成的影响, [思考 1、种群的逻辑斯谛增长中的K值是否是稳定不变的? 2、种群的逻辑斯谛增长曲线中、K两个参数的生物学意义是什么? 3、为什么说种群的逻辑斯谛增长是受到密度制约的? 6
6 (三)逻辑斯谛方程的拟合 1、通过做图目测估计法、平均值法、三点法等方法,计算或估计 K、 r、a 的值。 2、将每天的观测数据记录在自制的观测数据记录表格中。 (四)实验分组和讨论 1、实验分组 本实验可由学生分组进行,并可在不同的环境条件下进行对比实验。环境容 纳量也象其他生态特征一样,是随环境条件的不同而改变的。因此逻辑斯谛增长 曲线对于某一种生物也不是固定不变的。如改变培养温度,将草履虫培养液放置 在不同的培养温度下培养。对所得到的不同温度下的草履虫种群增长曲线,可以 让同学们来讨论环境条件的改变对草履虫实验种群增长的影响。 2、实验讨论 ①撰写实验报告,绘制草履虫实验种群的罗辑斯谛增长曲线。 ②讨论实验中各种实验条件的不同可能给草履虫种群增长造成的影响。 [思考题] 1、种群的逻辑斯谛增长中的 K 值是否是稳定不变的? 2、种群的逻辑斯谛增长曲线中 r、K 两个参数的生物学意义是什么? 3、为什么说种群的逻辑斯谛增长是受到密度制约的?

实验四种群数量估计 [实验原理 在种群中捕获一组动物样品,标记后放回,让标记动物与种群其它个体充分 混合后重取一组样品,则标记动物在第二组样品中所占比例与所有标记动物在整 个种群中占的比例相同:那么有m/n2=n,N其中n是第一次标记并放回的动物 数,是第二次样品中的动物数, 是第二次样品中已标记的动物数,N为种 很明显,n、m和m都是已知的,N可计算出来。所有标记重捕获) 实验目的 通过实验初步学会标记与重捕技术,即主要学习单次标记多次重捕技术一 Lincoln指数法和多次标记重捕技术一Jolly-Seber随机法估计动物种群数量的大 [实验材料] 里、白用棋子(代替实验动物),marker笔,100ml和50ml的烧杯、黑色 布袋。 (一)Lincoln指数法估计种群数量 Lincoln指数法的运用必须具备下列假设条件: 1、标记方法不能影响个体的正常活动: 2、标记保留的时间不能少于整个实验时间: 3、第二次取样之前标记个体必须在自然种群中充分混合: 4 不同年龄的个体具有相等的被捕几 5、种群是封闭的,即没有迁入或迁出,如果有,则迁入或迁出的数值 能够测定: 6、实验期间没有出生或死亡,如果有其数量则必须能够测定。 Lincoln指数法的基本公式:D/a=n 其中,p代表种群总数;a代表最初标记数:n代表取样总数:r样本中己标 记个体数 [方法与步骤] 1、每两人一小组,每小组取一个黑布袋,每袋装入实验教师发的白色围棋 子250个左右,但每组所装棋子数不等。 每组再分别装入黑色棋子50个左右(相当于标记),并记录具体数目(按 表) 3、将黑色棋子与布袋中原有的白棋子混合均匀。 4、用烧杯随机取一烧杯棋子,并记录黑棋子数和总棋子数。 5、重复步骤“4”4至5次。 6、计算p值。N一所取棋子(相当于样本)全总个数, 一样本中标记 的棋子个数(黑棋子数)。a -最初标记棋子数(总的黑棋子数) 注:取样计数过程中, 一半实验组用100ml的烧杯:另一半实验组用50ml的烧 杯。 7、各组按表4一1所示格式把实验结果进行汇总,计算布袋中所装棋子的
7 实验四 种群数量估计 [实验原理] 在种群中捕获一组动物样品,标记后放回,让标记动物与种群其它个体充分 混合后重取一组样品, 则标记动物在第二组样品中所占比例与所有标记动物在整 个种群中占的比例相同;那么有 m2/n2=n1/N 其中 n1 是第一次标记并放回的动物 数,n2 是第二次样品中的动物数,m2 是第二次样品中已标记的动物数,N为种 群总数。很明显,n1、n2 和 m2 都是已知的,N可计算出来。所有标记重捕获方 法均依赖于这一原理。 [实验目的] 通过实验初步学会标记与重捕技术,即主要学习单次标记多次重捕技术— Lincoln 指数法和多次标记重捕技术—JollySeber 随机法估计动物种群数量的大 小。 [实验材料] 黑、白围棋子(代替实验动物),marker 笔,100ml 和 50ml 的烧杯、黑色 布袋。 (一)Lincoln 指数法估计种群数量 Lincoln 指数法的运用必须具备下列假设条件: 1、标记方法不能影响个体的正常活动; 2、标记保留的时间不能少于整个实验时间; 3、第二次取样之前标记个体必须在自然种群中充分混合; 4、不同年龄的个体具有相等的被捕几率; 5、种群是封闭的,即没有迁入或迁出,如果有,则迁入或迁出的数值 能够测定; 6、实验期间没有出生或死亡,如果有其数量则必须能够测定。 Lincoln 指数法的基本公式:p/a=n/r 其中,p 代表种群总数;a 代表最初标记数;n 代表取样总数;r 样本中已标 记个体数。 [方法与步骤] 1、每两人一小组,每小组取一个黑布袋,每袋装入实验教师发的白色围棋 子 250 个左右,但每组所装棋子数不等。 2、每组再分别装入黑色棋子 50 个左右(相当于标记),并记录具体数目(按 表 1) 3、将黑色棋子与布袋中原有的白棋子混合均匀。 4、用烧杯随机取一烧杯棋子,并记录黑棋子数和总棋子数。 5、重复步骤“4”4 至 5 次。 6、计算 p 值。N——所取棋子(相当于样本)全总个数,r——样本中标记 的棋子个数(黑棋子数)。a——最初标记棋子数(总的黑棋子数); 注:取样计数过程中,一半实验组用 100ml 的烧杯;另一半实验组用 50ml 的烧 杯。 7、各组按表 4-1所示格式把实验结果进行汇总,计算布袋中所装棋子的
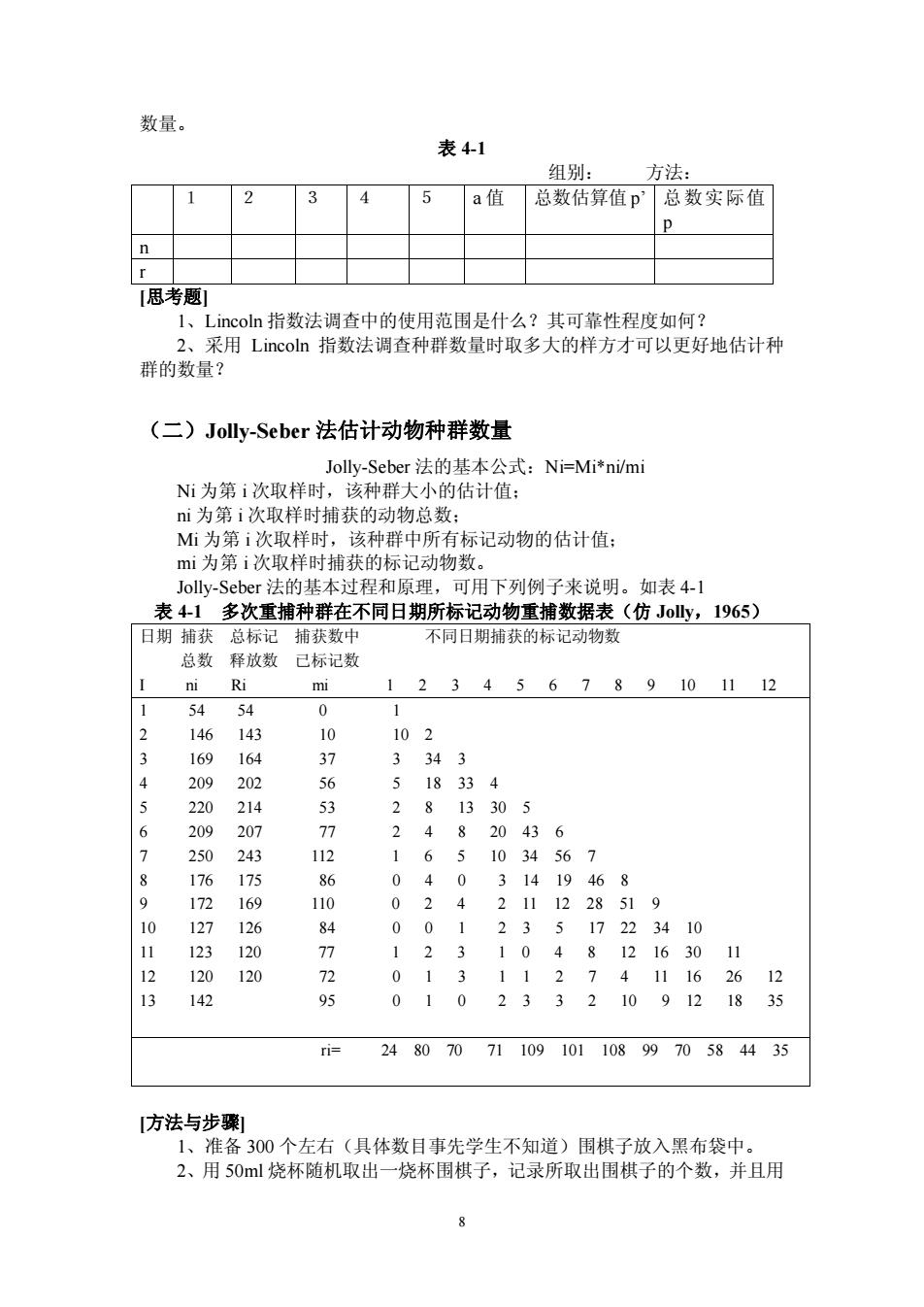
数量。 表41 组别: 方法 3 4 5 a值总数估算值p'总数实际值 思考题 I、Lincoln指数法调查中的使用范围是什么?其可靠性程度如何? 2、采用Lincoln指数法调查种群数量时取多大的样方才可以更好地估计种 群的数量? (二)Jolly-Seber法估计动物种群数量 Jolly-Seber法的基本公式:Ni=Mi*nimi Ni为第i次取样时,该种群大小的估计值: 为第1次取样时捕获的动物总数 M为第i次取样时,该种群中所有标记动物的估计值: mi为第i次取样时捕获的标记动物数。 Joly-Seber法的基本过程和原理,可用下列例子来说明。如表4-1 来多众黑箱种在不同日所标记动物裤数精来(仿,】 口期捕获总标记捕获数中 总数 释放数已标记费 RI mi 123456789101112 1 5454 0 1 146 143 10 102 164 37 3 343 4 205 202 56 18334 5 220 214 813305 6 209 207 24820436 7 250 243 112 1651034567 176 0 40 31419468 0 8108 8 211 2851 9 01 235 1722 410 3 120 123 104812163011 120 120 72 0131127411162612 13 142 0 10 2332109121835 ri= 248070711091011089970584435 [方法与步骤 1、准备300个左右(具体数目事先学生不知道)围棋子放入黑布袋中 2、用50ml烧杯随机取出一烧杯围棋子,记录所取出围棋子的个数,并且用
8 数量。 表 41 组别: 方法: 1 2 3 4 5 a 值 总数估算值 p’ 总数实际值 p n r [思考题] 1、Lincoln 指数法调查中的使用范围是什么?其可靠性程度如何? 2、采用 Lincoln 指数法调查种群数量时取多大的样方才可以更好地估计种 群的数量? (二)JollySeber 法估计动物种群数量 JollySeber 法的基本公式:Ni=Mi*ni/mi Ni 为第 i 次取样时,该种群大小的估计值; ni 为第 i 次取样时捕获的动物总数; Mi 为第 i 次取样时,该种群中所有标记动物的估计值; mi 为第 i 次取样时捕获的标记动物数。 JollySeber 法的基本过程和原理,可用下列例子来说明。如表 41 表 41 多次重捕种群在不同日期所标记动物重捕数据表(仿 Jolly,1965) 日期 捕获 总标记 捕获数中 不同日期捕获的标记动物数 总数 释放数 已标记数 I ni Ri mi 1 2 3 4 5 6 7 8 9 10 11 12 1 54 54 0 1 2 146 143 10 10 2 3 169 164 37 3 34 3 4 209 202 56 5 18 33 4 5 220 214 53 2 8 13 30 5 6 209 207 77 2 4 8 20 43 6 7 250 243 112 1 6 5 10 34 56 7 8 176 175 86 0 4 0 3 14 19 46 8 9 172 169 110 0 2 4 2 11 12 28 51 9 10 127 126 84 0 0 1 2 3 5 17 22 34 10 11 123 120 77 1 2 3 1 0 4 8 12 16 30 11 12 120 120 72 0 1 3 1 1 2 7 4 11 16 26 12 13 142 95 0 1 0 2 3 3 2 10 9 12 18 35 ri= 24 80 70 71 109 101 108 99 70 58 44 35 [方法与步骤] 1、准备 300 个左右(具体数目事先学生不知道)围棋子放入黑布袋中。 2、用 50ml 烧杯随机取出一烧杯围棋子,记录所取出围棋子的个数,并且用

记号笔在每个棋子上做一个记号,代表标记释放日期:然后将标记后的棋子再放 回布袋中,并与原有的棋子充分混匀。第二次再取出一烧杯,分别记录有标记的 棋子的数目和未标记棋子的数目:并对取出的未标记的棋子再做第二种标记,然 后将所取棋子放回布袋中,并 工分混匀。第 次再用烧杯随机取出棋子,分别记 录未标记棋子数和已标记棋子数,将取出的棋子再放入布袋中,并充分混匀。如 此重复13次,把每次取出的棋子数、放回数等按表4-1的格式记录下来。为弥 补动物出生和死亡的变化,实验过程中,实验指导教师可以随机以每个布袋中取 出一定量的棋子,同时再放入一定量的棋子,具体数目学生不得而知 根据表41中的数 6表 4、根据表41,4-2数据,按公式(1)·(4)分别估算标记动物总数Mi、 种群总数Ni、重捕比例ai并按表43进行分析。 公式:Zi/Mi-mi)=ri/Ri (2) ai=Mi/Ni=mi/ni (3) 附:模型中应用符号的说明 =捕获或取样的序号 N=第i次取样时该种群大小的估计值 ni=第i次取样时捕获的动物总数: M=第i次取样时,该种群中全部标记动物总数的估计值 =第ⅰ次取样时捕获的标记动物数: RF第i次释放的标记动物总数: =第i次标记的动物在以后的重捕总数:(日后重捕的Ri动物数) Z=在第i次之前标记的而在第i次之后(不包括第ⅰ次)重捕的数量: a=第i次取样时,种群中标记动物的比例 表42标记动物重捕积累统计表 捕获日期 2102 3 3 373 4523564 521023535 6 26 143477 6 7 2 22 36 1127 8 0 4 4 7 21 40 88 8 902 31 59 0 6 28 84 10 3 6 19 31 47 77 11 120 1 6 8 15 19 30 46 72 12 13 0 9 42 9513 Zi+1 89 12 23 Z4 Z6Z7 Z9 Z10 Z11 Z12 9
9 记号笔在每个棋子上做一个记号,代表标记释放日期;然后将标记后的棋子再放 回布袋中,并与原有的棋子充分混匀。第二次再取出一烧杯,分别记录有标记的 棋子的数目和未标记棋子的数目;并对取出的未标记的棋子再做第二种标记,然 后将所取棋子放回布袋中,并充分混匀。第三次再用烧杯随机取出棋子,分别记 录未标记棋子数和已标记棋子数,将取出的棋子再放入布袋中,并充分混匀。如 此重复 13 次,把每次取出的棋子数、放回数等按表 41 的格式记录下来。为弥 补动物出生和死亡的变化,实验过程中,实验指导教师可以随机以每个布袋中取 出一定量的棋子,同时再放入一定量的棋子,具体数目学生不得而知。 3、根据表 41 中的数据再填写表 42 4、根据表 41,42 数据,按公式(1)(4)分别估算标记动物总数 Mi、 种群总数 Ni、重捕比例 ai, 并按表 43 进行分析。 公式:Zi/(Mimi)=ri/Ri (2) ai=Mi/Ni=mi/ni (3) 附:模型中应用符号的说明 i=捕获或取样的序号 Ni=第 i 次取样时该种群大小的估计值; ni=第 i 次取样时捕获的动物总数; Mi=第 i 次取样时,该种群中全部标记动物总数的估计值; mi=第 i 次取样时捕获的标记动物数; Ri=第 i 次释放的标记动物总数; ri=第 i 次标记的动物在以后的重捕总数;(日后重捕的 Ri 动物数) Zi=在第 i 次之前标记的而在第 i 次之后(不包括第 i 次)重捕的数量; ai=第 i 次取样时,种群中标记动物的比例 表 42 标记动物重捕积累统计表 捕 获 日 期 1 2 10 2 3 3 37 3 4 5 23 56 4 5 2 10 23 53 5 6 2 6 14 34 77 6 7 1 7 12 22 56 112 7 8 0 4 4 7 21 40 88 8 9 0 2 6 8 19 31 59 110 9 10 0 0 1 3 6 11 28 50 84 10 11 1 3 6 7 7 11 19 31 47 77 11 捕 获 日 期 12 0 1 4 5 6 8 15 19 30 46 72 12 13 0 1 1 3 6 9 11 21 30 42 60 95 13 Zi+1 14 Z2 57 Z3 71 Z4 89 Z5 121 Z6 110 Z7 132 Z8 121 Z9 107 Z10 88 Z11 60 Z12
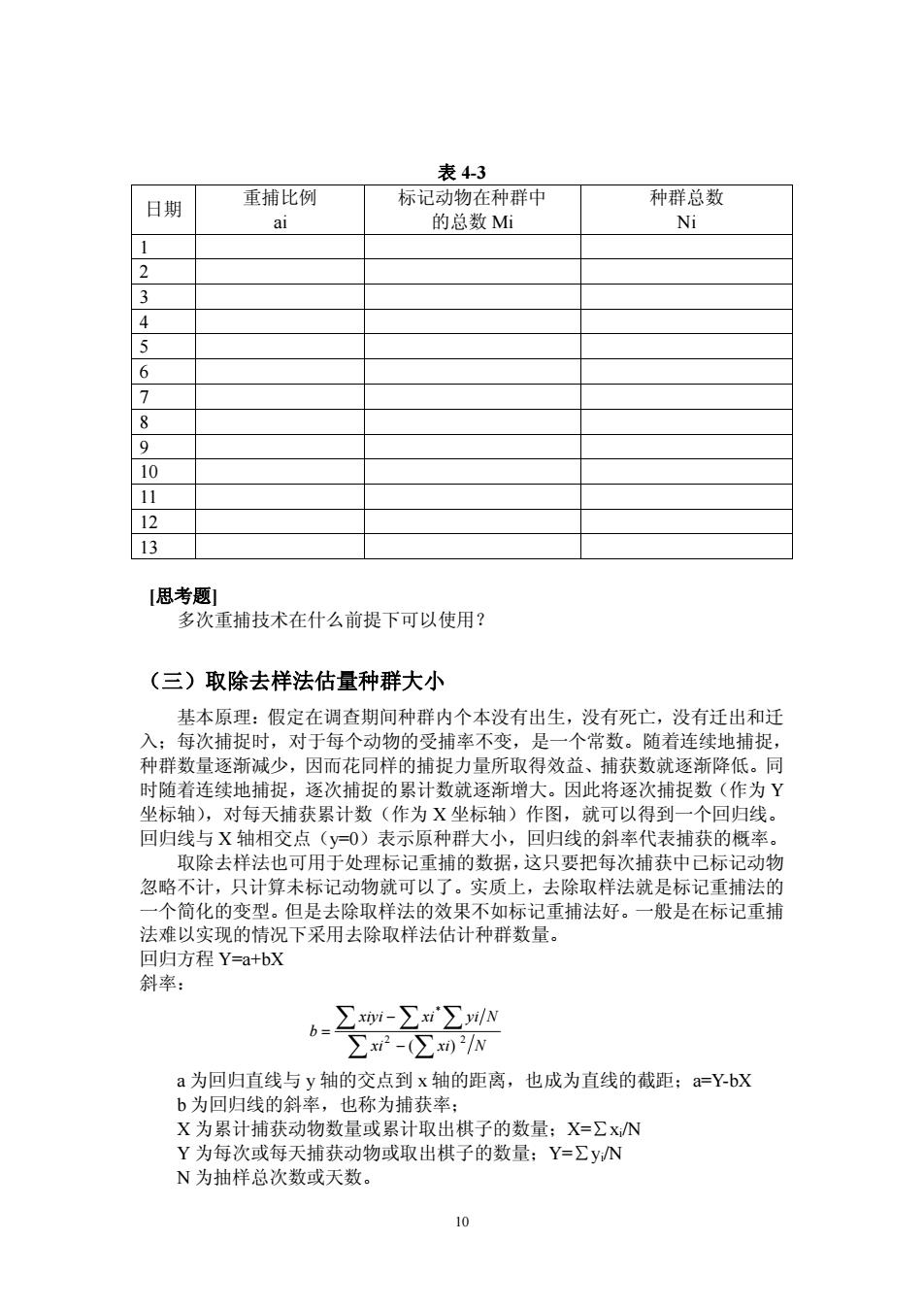
表43 日期 重捕比例 标记动物在种群中 种群总数 的总数Mi Ni 1 2 3 4 7 8 9 10 1 12 13 1思考题! 多次重捕技术在什么前提下可以使用? (三)取除去样法估量种群大小 基本原理:假定在调查期间种群内个本没有出生,没有死亡,没有迁出和迁 入;每次捕捉时,对于每个动物的受捕率不变,是一个常数。随着连续地捕捉, 种群数量逐渐减少,因而花同样的捕捉力量所取得效益、捕获数就逐渐降低。同 时随着连续地捕捉,逐次捕捉的累计数就逐渐增大。因此将逐次捕捉数(作为Y 坐标轴),对每天捕获累计数(作为X坐标轴)作图,就可以得到 一个回归线 回归线与X轴相交点(y0)表示原种群大小,回归线的斜率代表捕获的概率 取除去样法也可用于处理标记重捕的数据,这只要把每次捕获中已标记动物 忽略不计,只计算未标记动物就可以了。实质上,去除取样法就是标记重捕法的 一个简化的变型。但是去除取样法的效果不如标记重捕法好。一般是在标记重捕 法难以实现的情况下采用去除取样法估计种群数量。 回归方程Y=a+bx 斜率: ∑-∑x∑yN ∑x2-(∑x02N a为回归直线与y轴的交点到x轴的距离,也成为直线的截距;a=YbX b为回归线的斜率,也称为捕获率: X为累计捕获动物数量或累计取出棋子的数量:X=∑xN Y为每次或每天捕获动物或取出棋子的数量:Y=ΣyN N为抽样总次数或天数
10 表 43 日期 重捕比例 ai 标记动物在种群中 的总数 Mi 种群总数 Ni 1 2 3 4 5 6 7 8 9 10 11 12 13 [思考题] 多次重捕技术在什么前提下可以使用? (三)取除去样法估量种群大小 基本原理:假定在调查期间种群内个本没有出生,没有死亡,没有迁出和迁 入;每次捕捉时,对于每个动物的受捕率不变,是一个常数。随着连续地捕捉, 种群数量逐渐减少,因而花同样的捕捉力量所取得效益、捕获数就逐渐降低。同 时随着连续地捕捉,逐次捕捉的累计数就逐渐增大。因此将逐次捕捉数(作为 Y 坐标轴),对每天捕获累计数(作为 X 坐标轴)作图,就可以得到一个回归线。 回归线与 X 轴相交点(y=0)表示原种群大小,回归线的斜率代表捕获的概率。 取除去样法也可用于处理标记重捕的数据, 这只要把每次捕获中已标记动物 忽略不计,只计算未标记动物就可以了。实质上,去除取样法就是标记重捕法的 一个简化的变型。但是去除取样法的效果不如标记重捕法好。一般是在标记重捕 法难以实现的情况下采用去除取样法估计种群数量。 回归方程 Y=a+bX 斜率: Â Â Â Â Â - - = xi xi N xiyi xi yi N b 2 2 * ( ) a 为回归直线与 y 轴的交点到 x 轴的距离,也成为直线的截距;a=YbX b 为回归线的斜率,也称为捕获率; X 为累计捕获动物数量或累计取出棋子的数量;X=∑xi/N Y 为每次或每天捕获动物或取出棋子的数量;Y=∑yi/N N 为抽样总次数或天数