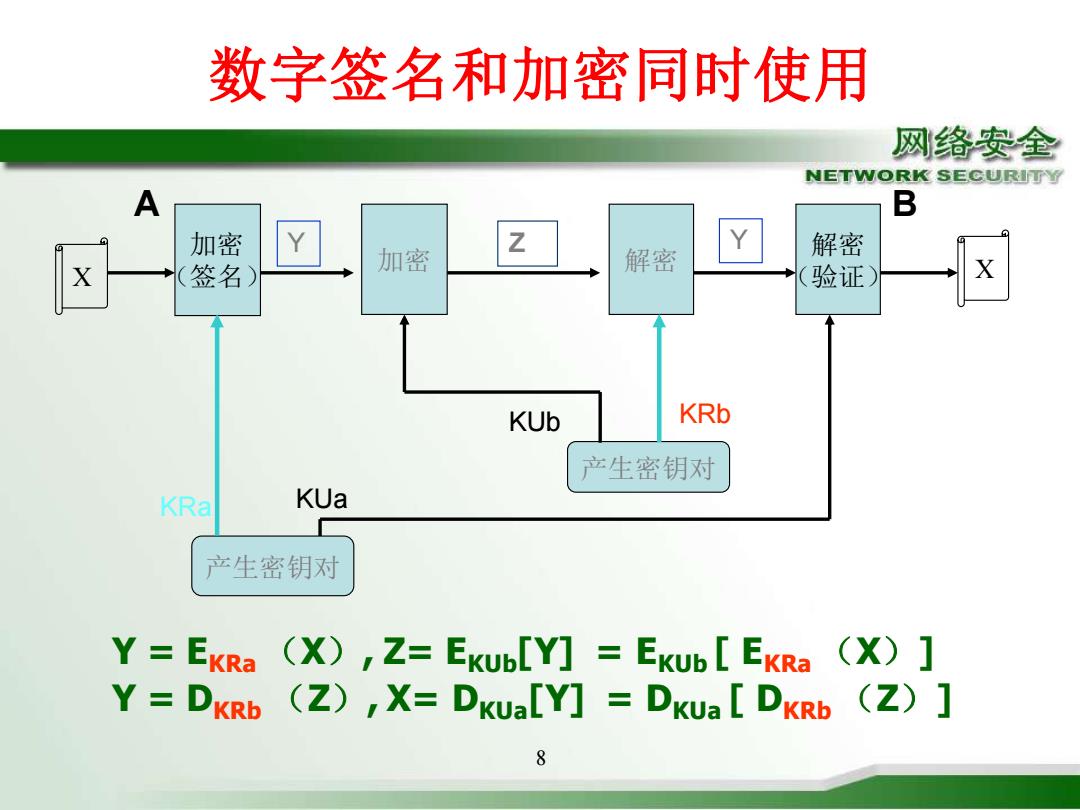
数字签名和加密同时使用 网络安全 NETWORK SECURITY A B 加密 加密 解密 Y 解密 签名 验证 X KUb KRb 产生密钥对 KRa KUa 产生密钥对 Y=EKRa (X),Z=EKUb[Y]EKUb EKRa (X)] Y=DKRb (Z)X=DKUa[Y]DKUa DKRb (Z)] 8
8 X 加密 (签名) 加密 解密 解密 (验证) X Y Z Y = EKRa (X), Z= EKUb[Y] = EKUb [ EKRa (X)] Y = DKRb (Z), X= DKUa[Y] = DKUa [ DKRb (Z)] A B 产生密钥对 产生密钥对 KRa KUa KUb KRb 数字签名和加密同时使用 Y

基本思想和要求 网络安全 NETWORK SECURITY ·涉及到各方:发送方、接收方、攻击者 ·涉及到数据:公钥、私钥、明文、密文 ·公钥算法的条件: ·产生一对密钥是计算可行的 ·已知公钥和明文,产生密文是计算可行的 ·接收方利用私钥来解密密文是计算可行的 ·对于攻击者,利用公钥来推断私钥是计算不可行的 已知公钥和密文,恢复明文是计算不可行的 ·(可选)加密和解密的顺序可交换 9
9 基本思想和要求 • 涉及到各方:发送方、接收方、攻击者 • 涉及到数据:公钥、私钥、明文、密文 • 公钥算法的条件: ▪ 产生一对密钥是计算可行的 ▪ 已知公钥和明文,产生密文是计算可行的 ▪ 接收方利用私钥来解密密文是计算可行的 ▪ 对于攻击者,利用公钥来推断私钥是计算不可行的 ▪ 已知公钥和密文,恢复明文是计算不可行的 ▪ (可选)加密和解密的顺序可交换

如何设计一个公钥算法 网络安全 NETWORK SECURITY ·公钥和私钥必须相关,而且从公钥到私钥不可 推断 ·必须要找到一个难题,从一个方向走是容易的, 从另一个方向走是因难的 ·如何把这个难题跟加解密结合起来 ·计算可行和不可行的界 10
10 如何设计一个公钥算法 • 公钥和私钥必须相关,而且从公钥到私钥不可 推断 ▪ 必须要找到一个难题,从一个方向走是容易的, 从另一个方向走是困难的 ▪ 如何把这个难题跟加解密结合起来 • 计算可行和不可行的界

公钥密码学的研究情况 网络安全 NETWORK SECURITY ·与计算复杂性理论密切相关 ·计算复杂性理论可以提供指导 ·但是需求不尽相同 >计算复杂性通常针对一个孤立的问题进行研究 >而公钥密码学往往需要考虑一些相关的问题 比如,密码分析还需要考虑已知明文、选择明文等相关的情形 ·讨论的情形不同 >计算复杂性考虑最坏的情形 >而对于公钥密码学则是不够的 ·,一个困难问题必然会导致一个保密性很好的密码系统吗? ·不一定,还需要有好的构造 11
11 公钥密码学的研究情况 • 与计算复杂性理论密切相关 • 计算复杂性理论可以提供指导 ▪ 但是需求不尽相同 ➢ 计算复杂性通常针对一个孤立的问题进行研究 ➢ 而公钥密码学往往需要考虑一些相关的问题 比如,密码分析还需要考虑已知明文、选择明文等相关的情形 ▪ 讨论的情形不同 ➢ 计算复杂性考虑最坏的情形 ➢ 而对于公钥密码学则是不够的 • 一个困难问题必然会导致一个保密性很好的密码系统吗? ▪ 不一定,还需要有好的构造

RSA算法简介 网络安全 NETWORK SECURITY ·77年发明,78年公布 。Ron Rivest,Adi Shamir,Leonard Adleman(这是 三位发明人) ·RSA的安全性基于大数分解的难度 ·RSA在美国申请了专利(2000年9月已经到期),在其 他国家没有 ·RSA已经成了事实上的工业标准,在美国除外 12
12 RSA算法简介 • 77年发明,78年公布 • Ron Rivest, Adi Shamir , Leonard Adleman (这是 三位发明人) • RSA的安全性基于大数分解的难度 • RSA在美国申请了专利(2000年9月已经到期),在其 他国家没有 • RSA已经成了事实上的工业标准,在美国除外