
2.4闭▣系统的拥平衡方程与㶲损失 入一 ExL=Exo+(Eu-Eu,)-Ew (出+损失)=增量 热源T =Ex.Q-AEsU-WA AExu=Esd;-Esu=(U2-U)+Po(V:-V)-To(S:-S) W=w.+po(2-) Ex9-00 Ex.=WA=W-Po(V2-V) 环境I。 W,=∫01-2)+E-E-E =∫广δ01-)+U,-U,+p-)-T(S-S)-Ex W4x=o01-2)+E,-E WA=WAmI-Ex.L W<WA.mas 10
10 入—(出+损失)=增量 2.4 闭口系统的㶲平衡方程与㶲损失 1 2 , , , , , , ( ) x L x Q x U x U W x Q x U A E E E E E E E W = + − − = − − 2 1 , , , 2 1 0 2 1 0 2 1 ( ) ( ) ( ) = − = − + − − − E E E U U p V V T S S x U x U x U , 0 2 1 ( ) E W W p V V x W A = = − − 0 1 2 0 2 , , , 1 2 1 2 0 1 2 0 1 2 , 1 (1 ) (1 ) ( ) ( ) H H T A x U x U x L T T T x L W Q E E E Q U U p V V T S S E = − + − − = − + − + − − − − 0 1 2 2 ,max , , 1 (1 ) H T W Q E E A x U x U T = − + − W W E A A x L = − ,max , W W A A ,max

2.4闭口系统的㶲平衡方程与㶲损失 入一(出+损失)=增量 形4x=ò01-0)+E山-E, 热源T Ex.L=WA.ma -WA W=Wu+po(V2-Vi) W=(Q+9)-△U =0 Ex.e0-02o W=Wa+PoAV=Wa+Po(V2-V) 环境T。 EL=∫δ01-)+(U,-U2)+p心-'2)- T(S-S2)-(Q+Q)-△U-P(%-)】 =T(S-S)-∫δ0-Q 11
11 入—(出+损失)=增量 2.4 闭口系统的㶲平衡方程与㶲损失 0 1 2 2 ,max , , 1 (1 ) H T W Q E E A x U x U T = − + − E W W x L A A , ,max = − 0 W Q Q U = + − ( )0 0 2 1 ( ) W W p V W p V V = + = + − A A 0 0 2 , 1 2 0 1 2 1 0 1 2 0 0 2 1 0 2 1 0 (1 ) ( ) ( ) ( ) [( ) ( )] ( ) H H T x L T T T E Q U U p V V T S S Q Q U p V V T S S Q Q = − + − + − − − − + − − − = − − −
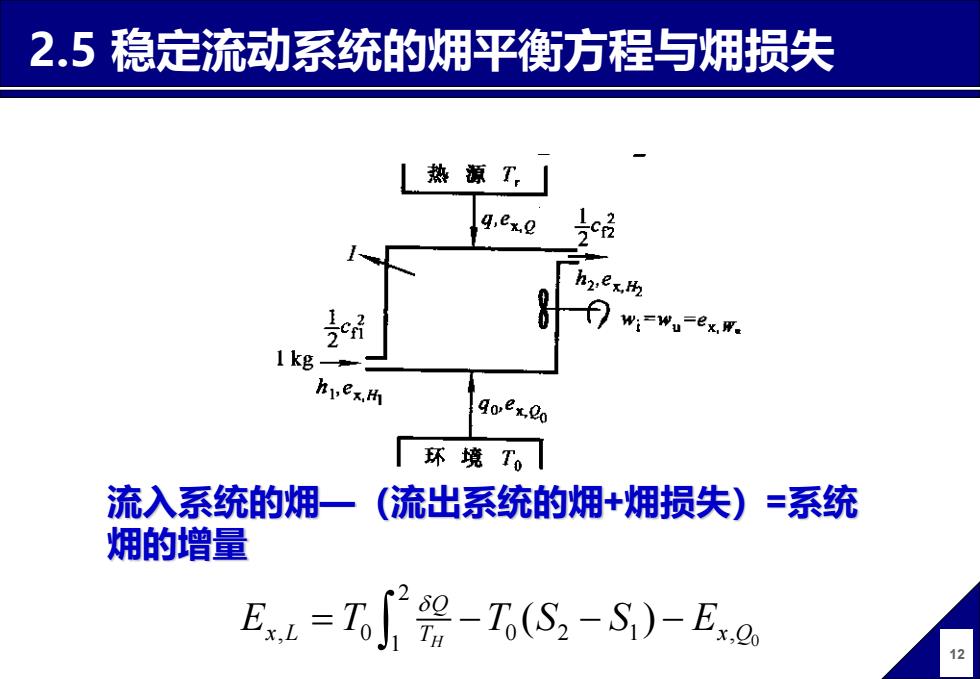
2.5稳定流动系统的拥平衡方程与拥损失 L热源工,」 9.ex.o w:-wu-ex.w. I kg hex. goex.Co 环境T。 流入系统的㶲一(流出系统的㶲+㶲损失)=系统 㶲的增量 器-IS,-S)-Ee 12
12 流入系统的㶲—(流出系统的㶲+㶲损失)=系统 㶲的增量 2.5 稳定流动系统的㶲平衡方程与㶲损失 0 2 , 0 0 2 1 , 1 ( ) H Q E T T S S E x L x Q T = − − −

2.6循环系统的㶲平衡方程式与㶲损失分析 流入系统的㶲一(流出系统的㶲+㶲损失)=系统 㶲的增量 Ex.0-(Exw+Ex)=0 Ex0=$(1-号)60 Esw=$8W $1-)62=$oW4+E 13
13 流入系统的㶲—(流出系统的㶲+㶲损失)=系统 㶲的增量 2.6 循环系统的㶲平衡方程式与㶲损失分析 , , , ( ) 0 E E E x Q x W x L − + = 0 , (1 ) T E Q x Q T = − ∮ E W x W, =∮ 0 , (1 ) T T Q W E A x L ∮ − = + ∮

2.6.1动力循环 入一(出+损失)=增量 㶲平衡方程 $l-)δ0=5δW4+E2 TH热源 δ01-)-∫0(I-2)-W4=EL Q Jn识mI-) mams=n0l-)-∫0.0-2) Wa EX WA=WAMaX -Ex.L ∫0.1-) 当,=时 W4=∫nδ0aI-)-EL 冷源T W4ns=∫òO(1-) 2=W4+=W4+Qo a-0.0-2-,=g-g-a4<0
14 TH 热源 E 冷源 TL WA QH QL EXl 㶲平衡方程 入—(出+损失)=增量 2.6.1 动力循环 0 , (1 ) T T Q W E A x L ∮ − = + ∮ 0 0 , (1 ) (1 ) H L T T H L A x L T T H L Q Q W E − − − − = 0 0 ,max (1 ) (1 ) H L T T A H L T T H L W Q Q = − − − W W E A A x L = − ,max , 当T T 0 = L时 0 , (1 ) H T A H x L T H W Q E = − − 0 ,max (1 ) H T A T H W Q = − Q W Q W Q H A L A = + = + 0 0 , 0 0 0 , 0 (1 ) H H H Q x L H A n Q T H H T E Q W Q T Q A Q T = − − = − = − 0 (1 ) H T H T H Q − 0 (1 ) L T L T L Q −