
例子 。∑={a,b} ·L(aIb)={a,b} 。 L((a I b)(a I b))={aa,ab,ba,bb} L(a")=s,a,aa,aaa,aaaa,.. L((a I b))={E,a,b,aa,ab,ba,bb,aaa,aab,... L(a I a"b)=a,b,ab,aab,aaab,.. 16
例子 • Σ = { a, b } • L(a | b) = { a, b } • L((a | b) (a | b)) = { aa, ab, ba, bb } • L(a* ) = { ε, a, aa, aaa, aaaa, … } • L((a | b)* ) = { ε, a, b, aa, ab, ba, bb, aaa, aab, … } • L(a | a*b) = { a, b, ab, aab, aaab, … } 16
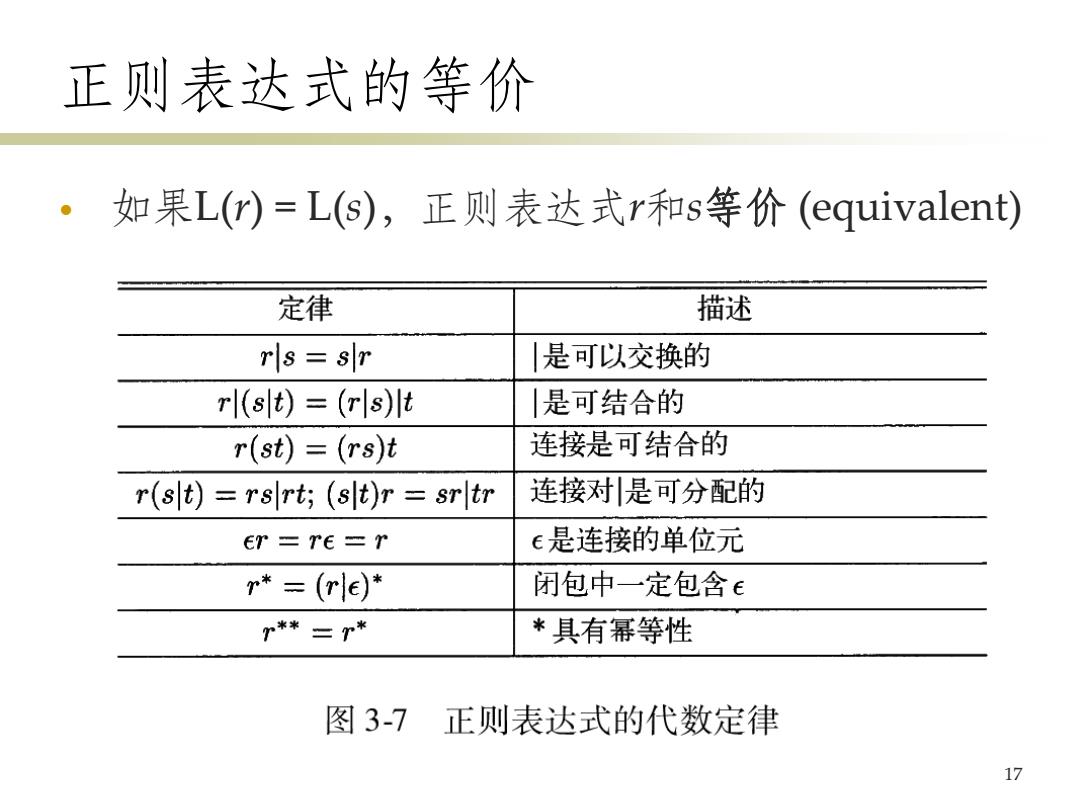
正则表达式的等价 如果L(r)=L(s),正则表达式r和s等价(equivalent) 定律 描述 rls =sr 是可以交换的 r (st)(rls)t 是可结合的 r(st)=(rs)t 连接是可结合的 r(st)=rsrt;(st)r srtr 连接对是可分配的 er Te=T e是连接的单位元 r*(rle)* 闭包中一定包含E r*二T* *具有幂等性 图3-7正则表达式的代数定律 17
正则表达式的等价 • 如果L(r) = L(s),正则表达式r和s等价 (equivalent) 17

正则定义(1) 为了书写方便,可以给正则表达式命名 。 正则定义(regular definition)是如下的定义序列: d1→r1 d2今r2 dn→rn 。其中 d:不在Σ中,且各不相同 每个r是字母表∑U{dvd2,,d1}上的正则表达式; 这保证了不会出现递归定义 18
正则定义 (1) • 为了书写方便,可以给正则表达式命名 • 正则定义 (regular definition) 是如下的定义序列: d1 → r1 d2 → r2 … dn → rn • 其中 – di不在Σ中,且各不相同 – 每个ri是字母表Σ { d1 , d2 , …, di-1 }上的正则表达式; 这保证了不会出现递归定义 18

正则定义(2) ·各个d;的∑上的正则表达式如下 d的正则表达式即r1 将r2中的d1替换为r1,得到d2的正则表达式 将r:中的dvd2,,d1替换为各自的正则表达式,得到d 的正则表达式 19
正则定义 (2) • 各个di的Σ上的正则表达式如下 – d1的正则表达式即r1 – 将r2中的d1替换为r1,得到d2的正则表达式 – … … – 将ri中的d1 , d2 , …, di-1替换为各自的正则表达式,得到di 的正则表达式 19

例子 ·C语言标识符的正则定义 letter >A I B I...I Z I a I b l...IzI digit→0111..19 id>letter(letter_I digit 。id对应的正则表达式为 (A I B I ..IZ I a l b l...I z )((A I B I ...IZ I a 1b1..1z1)1(0111..19)) 20
例子 • C语言标识符的正则定义 – letter_ → A | B | … | Z | a | b | … | z | _ – digit → 0 | 1 | … | 9 – id → letter_ ( letter_ | digit ) * • id对应的正则表达式为 – (A | B | … | Z | a | b | … | z | _) ( (A | B | … | Z | a | b | … | z | _) | (0 | 1 | … | 9) )* 20