9.2一阶有源滤波器 一阶有源低通滤波器 幅频特性:令: RC 4(jo)=(1+ 1+ H 其中 Amax =(1+ Ya(jo) .0o=1+ R+ joC R V.(jo) 1+joRC 4Ao)= V.(jo) 1+3 .(0o) R 1+joRC 传递函数中出现o的一次项,故 一 阶滤波器幅频特性曲线 称为一阶滤波器。 边沿平滑,滤波效果差
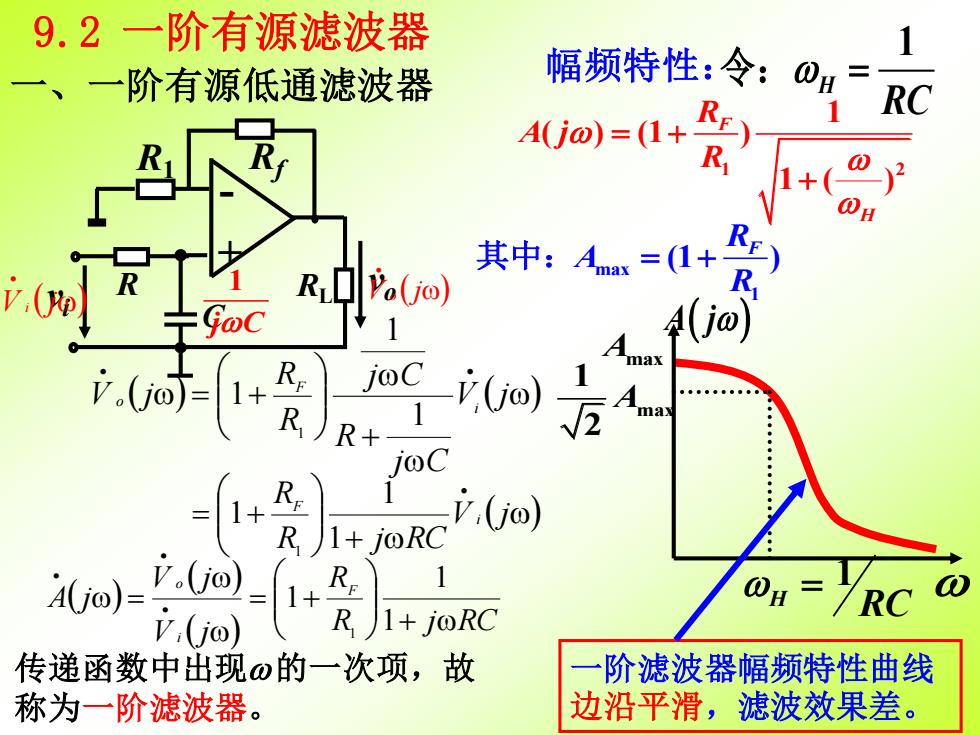
一、一阶有源低通滤波器 传递函数中出现的一次项,故 称为一阶滤波器。 v vo i R R1 + - RL Rf C 1 j C 1 2 1 ( ) (1 ) 1 ( ) F H R A j R = + + 幅频特性: 1 H RC 令: = 1 H RC = max 1 2 A A j ( ) Amax 9.2 一阶有源滤波器 一阶滤波器幅频特性曲线 边沿平滑,滤波效果差。 max 1 (1 ) RF A R 其中: = + ( ) • V i j ( ) • V o j ( ) ( ) + = + • • V j j C R j C R R V j i F o 1 1 1 1 ( ) + = + • V j R j RC R i F 1 1 1 1 ( ) ( ) ( ) R j RC R V j V j A j F i o + = + = • • • 1 1 1 1

二、一阶有源高通滤波器 幅频特性: Aj@)=(1+ + A(j) V(jo) 1 ,(Uo) 令:0= j@RC RC V.(jo 1+) 阶滤波器幅频特性曲线 ,(o 边沿平滑,滤波效果差
A j ( ) 0 L 二、一阶有源高通滤波器 vi C vo 1 j C 1 2 1 ( ) (1 ) 1 ( ) F L R A j R = + + 幅频特性: 1 L RC 令: = 一阶滤波器幅频特性曲线 边沿平滑,滤波效果差。 R R1 + - RL Rf ( ) • V i j ( ) • V o j ( ) ( ) + = + • • V j j C R R R R V j i F o 1 1 1 ( ) + = + • V j j RC R R i F 1 1 1 1 1 ( ) ( ) ( ) − = + = • • • L F i o j R R V j V j A j 1 1 1 1
9.3高阶有源滤波器 以二阶有源低通滤波器为例 R V.RW 1/joC立4三 v R+1/joC 1+joRC -==V+'-。 R R 1/joC 解出: 其中 Aj)= Vo 1 = Q。 (3-AE) 传递函数中出现ω的二次项,故称为二阶滤波器
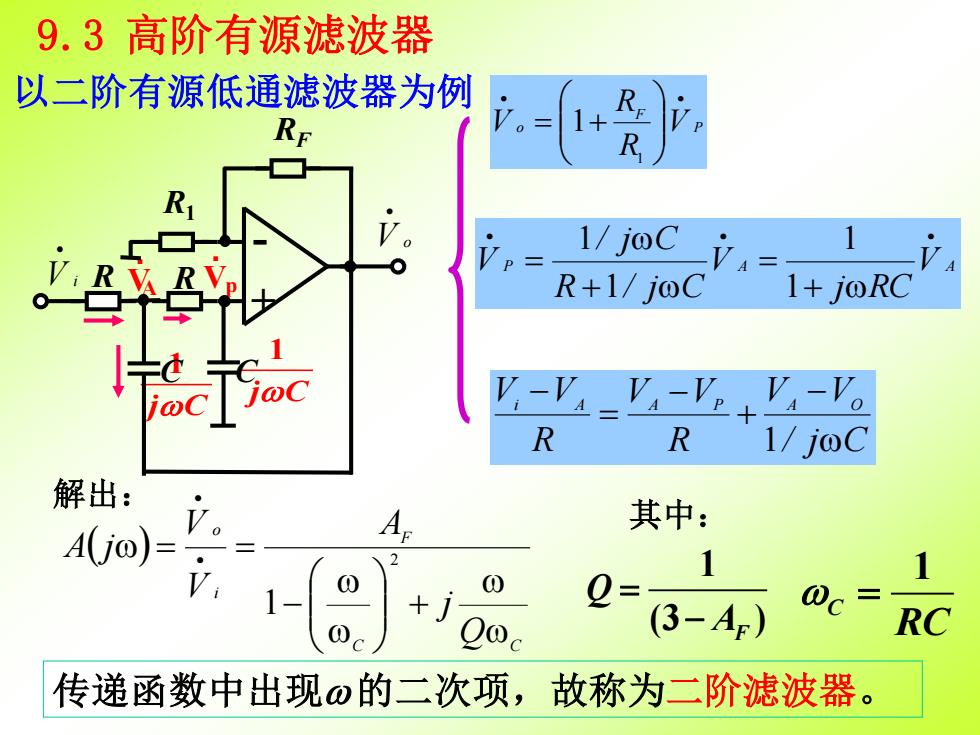
解出: 1 (3 ) F Q A = − 1 C RC = 其中: 以二阶有源低通滤波器为例 传递函数中出现 的二次项,故称为二阶滤波器。 9.3 高阶有源滤波器 VA . Vp . 1 j C 1 j C C C P F o V R R V • • = + 1 1 P A V A j RC V R / j C / j C V • • • + = + = 1 1 1 1 / j C V V R V V R Vi VA A P A O − + − = − 1 ( ) C C F i o Q j A V V A j + − = • = • 2 1 R R1 RF R + - V i • V o •
'A@)= A V ∴.A(j@= A(jo - 理想 一阶 低通 低通 二阶 低通 0 阶数越高,幅频特性曲线的边沿越陡,越接近理想滤波器
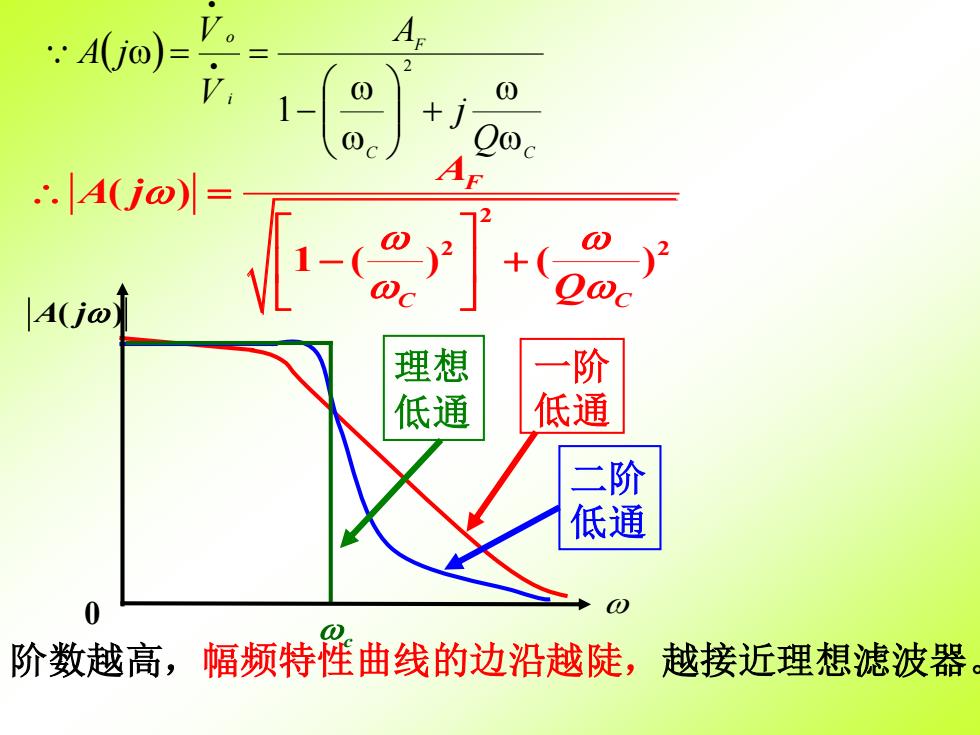
2 2 2 ( ) 1 ( ) ( ) F C C A A j Q = − + c A j ( ) 0 一阶 低通 二阶 低通 理想 低通 阶数越高,幅频特性曲线的边沿越陡,越接近理想滤波器。 ( ) C C F i o Q j A V V A j + − = • = • 2 1
9.4正弦波振荡电路的振荡条件 1.振荡条件 基本放大 正反馈放大电路框图 电路A (注意与负反馈方框图的差别) 文=文+, 反馈网络 户 若环路增益A疗=1则文,=水, 去掉文,文仍有稳定的输出。 又AF=AF∠p,+p,=AF∠p+p: 所以振荡条件为 「A()F(o)=1 振幅平衡条件 p(o)+p(⊙)=2nm相位平衡条件
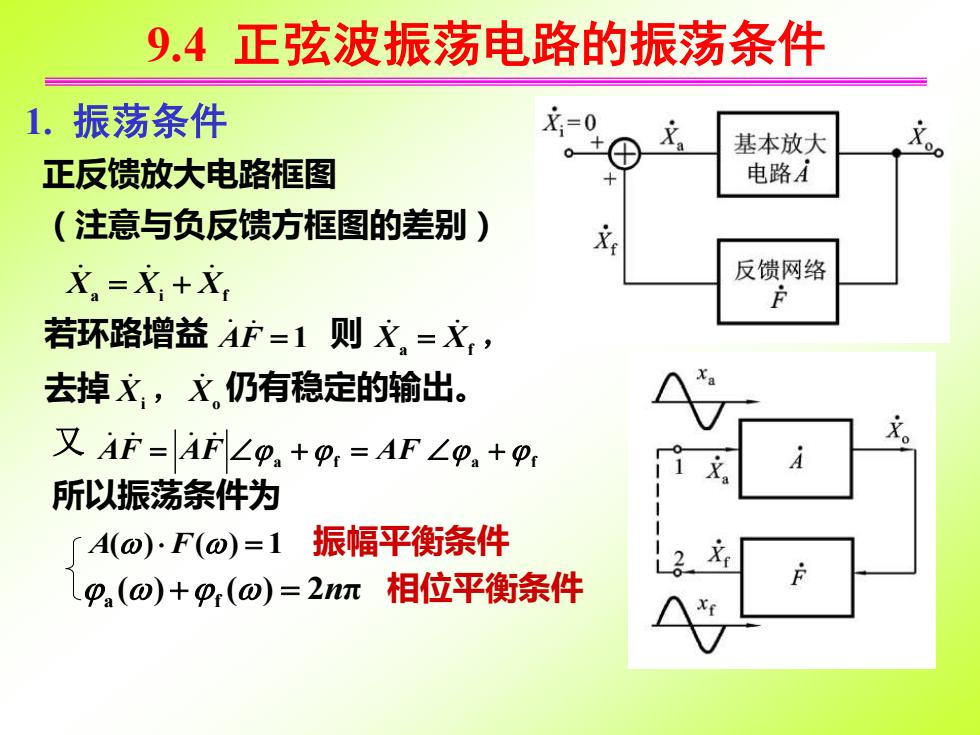
9.4 正弦波振荡电路的振荡条件 正反馈放大电路框图 (注意与负反馈方框图的差别) 1. 振荡条件 Xa Xi Xf = + 若环路增益 AF = 1 则 X a = X f , 去掉 X i , Xo 仍有稳定的输出。 又 AF = AF a + f = AF a + f 所以振荡条件为 A() F() = 1 振幅平衡条件 a () +f () = 2nπ 相位平衡条件