
Design of linear-phase FIR filters using windows Digital Signal Processing--FIR Digital Filter Design h(n)=d(n-M)= sin(wc(n-M)) π(n-M) Example: Determine the length-11,rectangularly windowed impulse response that ap-proximates (a)an ideal lowpass filter of cutoff frequency wc =T/4,(b) the ideal differen-tiator filter,and(c)the ideal Hilbert transformer filter d(k)= sin(πk/4) With N=11,we have M=(N-1)/2=5 , for-5≤k≤5 πk (a)an ideal lowpass filter of rectangular window 0,-10 (b)the ideal differen-tiator filter d(k)=cos(πk)s in(πk) k nk2 (c)the ideal Hilbert transformer filter d(k)= 1-Cos(πk) 2 πk =a=[品 0,-20, 品品别]上泽道大
Design of linear-phase FIR filters using windows Digital Signal Processing—— FIR Digital Filter Design Determine the length-11, rectangularly windowed impulse response that ap-proximates (a) an ideal lowpass filter of cutoff frequency ωc = π/4, (b) the ideal differen-tiator filter, and (c) the ideal Hilbert transformer filter Example: With N = 11, we have M = (N − 1)/2 = 5 (a) an ideal lowpass filter of rectangular window (b) the ideal differen-tiator filter (c) the ideal Hilbert transformer filter

Bartlett Window Digital Signal Processing--FIR Digital Filter Design The main problem associated with the rectangular window is 2n the presence of N-1 0≤n≤(N-I) ripples near the band 0B(n)= 2n edges of the resulting filter,which are 2-N- caused by the existence of sidelobes in the frequency response of the N.sin(@) .N-1 -0 window. Triangular window Wo(e)=sin(o12) has only small discontinuities near its edges,so it improves the ripples. 上游充通大
Digital Signal Processing—— FIR Digital Filter Design Bartlett Window The main problem associated with the rectangular window is the presence of ripples near the band edges of the resulting filter, which are caused by the existence of sidelobes in the frequency response of the window. Triangular window has only small discontinuities near its edges, so it improves the ripples. 2 1 , 0 ( 1) 1 2 ( ) 2 1 2 , ( 1) 1 1 2 Br n n N N n n N n N N 1 ( ) 2 2 sin( ) 4 ( ) [ ] 2 sin( / 2) N j j Br N N W e e

Hamming and Hanning windows Digital Signal Processing--FIR Digital Filter Design w,=--go1 0≤n≤M 0 otherwise The generalized Hamming window is defined as parameter 0≤a≤1. If a=0.54,it's Hamming window. If a=0.5,it's Hanning window. All three components have zeros close to o=+4n/(M+1). Hence,the mainlobetotal width is 8n/(M+1). 女 When a=0.54,the mainlobe total energy is approximately 99.96%of the window total energy. The transition band of Hamming window is larger than that of the rectangular window. The ratio between the main and first side lobes is 40dB, much larger than rectangular window. 上游充通大
Digital Signal Processing—— FIR Digital Filter Design Hamming and Hanning windows The generalized Hamming window is defined as parameter 0≤α≤1. If α=0.54, it’s Hamming window. If α=0.5, it’s Hanning window. All three components have zeros close to ω=±4π/(M+1). Hence, the mainlobetotal width is 8π/(M+1). When α=0.54, the mainlobe total energy is approximately 99.96% of the window total energy. The transition band of Hamming window is larger than that of the rectangular window. The ratio between the main and first side lobes is 40dB, much larger than rectangular window

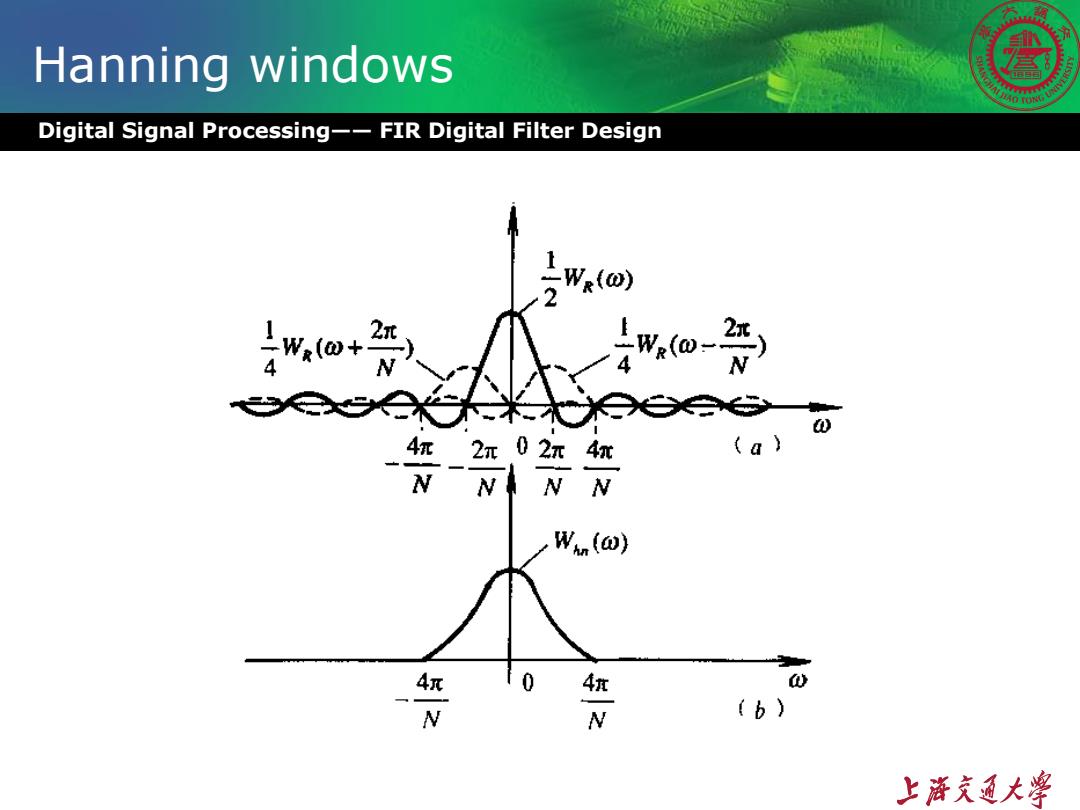
Hanning windows Digital Signal Processing--FIR Digital Filter Design o.闭=051-ca2R(W .e)=FIR,(mjl=paoe令' ()-F7W.(m)-t0.SF.()+2 1形,o:宁以o学 W- -0 Wao)=05w.o)+024a-2)+wao+2】 上游充通大¥
Digital Signal Processing—— FIR Digital Filter Design Hanning windows 1 2 1 1 2 2 2 ( ) 0.5[1 cos( )] ( ) 1 ( ) [ ( )] ( ) 2 ( ) [ ( )] {0.5 ( ) 0.25[ ( ) 1 2 ( )]} ( ) 1 Hn N N j j R N R j Hn Hn R R N N j j R Hn n n R n N W e FT R n W e W e FT W n W W N W e W e N 2 2 ( ) 0.5 ( ) 0.25[ ( ) ( )] W W W W Hn R R R N N
Hanning windows Digital Signal Processing--FIR Digital Filter Design WRo) 4 4 0 4红2π 02π4r (a) Wn(ω) 4π 0 4π N N (b) 上游充通大
Digital Signal Processing—— FIR Digital Filter Design Hanning windows