
1.1 What are neural networks? Let us commence with a provisional definition of what is meant by a "neural network"and follow with simple,working explanations of some of the key terms in the definition. A neural network is an interconnected assembly of simple processing elements,units or nodes,whose functionality is loosely based on the animal neuron.The processing ability of the network is stored in the interunit connection strengths,or weights,obtained by a process of adaptation to,or learning from,a set of training patterns. To flesh this out a little we first take a quick look at some basic neurobiology.The human brain consists of an estimated 1011(100 billion)nerve cells or neurons,a highly stylized example of which is shown in Figure 11.Neurons communicate via electrical signals that are short-lived impulses or"spikes"in the voltage of the cell wall or membrane.The interneuron connections are mediated by electrochemical junctions called synapses,which are located on branches of the cell referred to as dendrites.Each neuron typically receives many thousands of connections from Dendrites Synapses ceboh Axon Signal flow →nput ◆Output Figure 1.1 Essential components of a neuron shown in stylized form. other neurons and is therefore constantly receiving a multitude of incoming signals, which eventually reach the cell body.Here,they are integrated or summed together in some way and,roughly speaking,if the resulting signal exceeds some threshold then the neuron will "fire"or generate a voltage impulse in response.This is then transmitted to other neurons via a branching fibre known as the axon. In determining whether an impulse should be produced or not,some incoming signals produce an inhibitory effect and tend to prevent firing,while others are excitatory and promote impulse generation.The distinctive processing ability of each neuron is then supposed to reside in the type-excitatory or inhibitory-and strength of its synaptic connections with other neurons 13
1.1 What are neural networks? Let us commence with a provisional definition of what is meant by a "neural network" and follow with simple, working explanations of some of the key terms in the definition. A neural network is an interconnected assembly of simple processing elements, units or nodes, whose functionality is loosely based on the animal neuron. The processing ability of the network is stored in the interunit connection strengths, or weights, obtained by a process of adaptation to, or learning from, a set of training patterns. To flesh this out a little we first take a quick look at some basic neurobiology. The human brain consists of an estimated 10 11 (100 billion) nerve cells or neurons, a highly stylized example of which is shown in Figure 1.1. Neurons communicate via electrical signals that are short-lived impulses or "spikes" in the voltage of the cell wall or membrane. The interneuron connections are mediated by electrochemical junctions called synapses, which are located on branches of the cell referred to as dendrites. Each neuron typically receives many thousands of connections from Figure 1.1 Essential components of a neuron shown in stylized form. other neurons and is therefore constantly receiving a multitude of incoming signals, which eventually reach the cell body. Here, they are integrated or summed together in some way and, roughly speaking, if the resulting signal exceeds some threshold then the neuron will "fire" or generate a voltage impulse in response. This is then transmitted to other neurons via a branching fibre known as the axon. In determining whether an impulse should be produced or not, some incoming signals produce an inhibitory effect and tend to prevent firing, while others are excitatory and promote impulse generation. The distinctive processing ability of each neuron is then supposed to reside in the type—excitatory or inhibitory—and strength of its synaptic connections with other neurons. 13
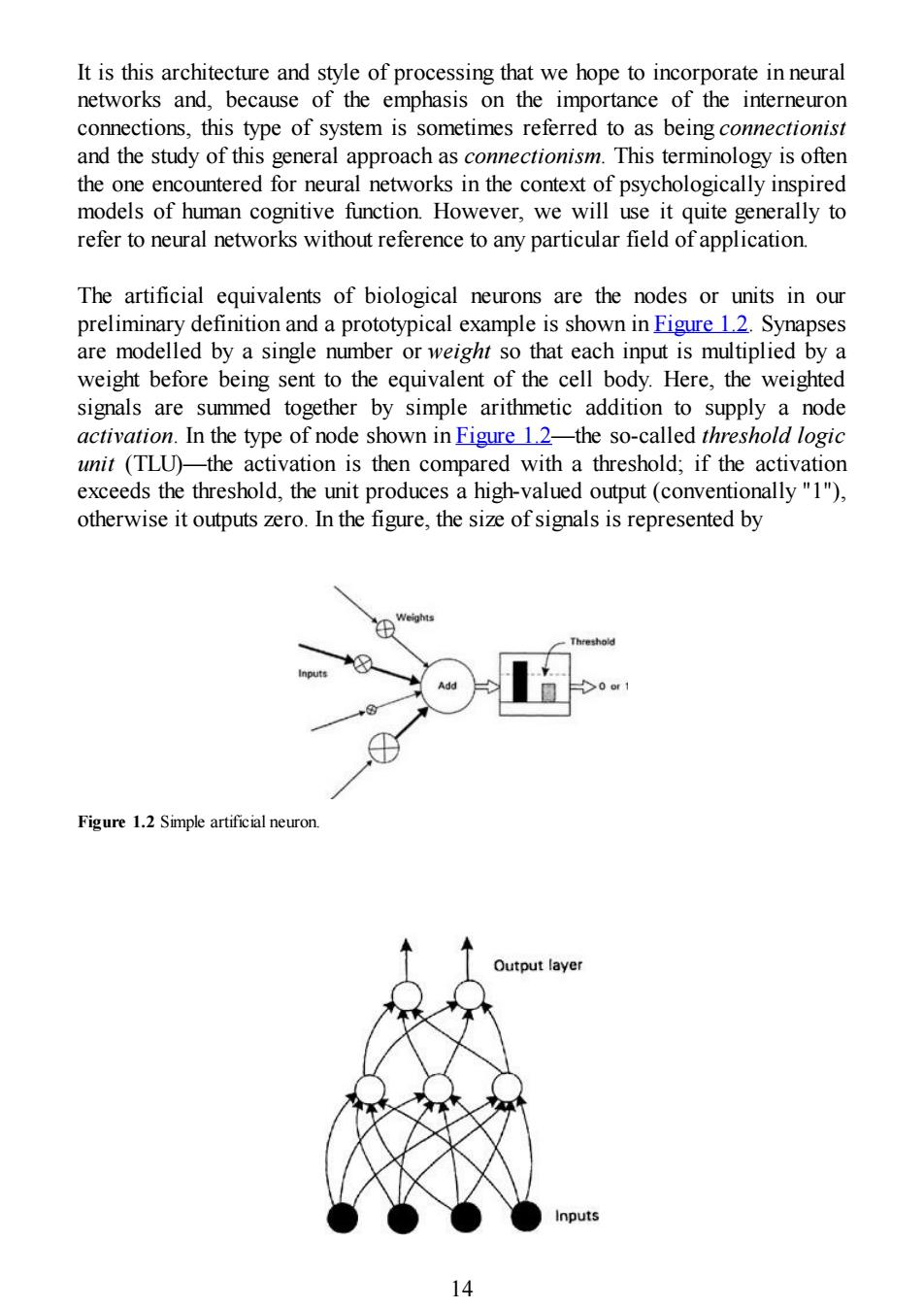
It is this architecture and style of processing that we hope to incorporate in neural networks and,because of the emphasis on the importance of the interneuron connections,this type of system is sometimes referred to as being connectionist and the study of this general approach as connectionism.This terminology is often the one encountered for neural networks in the context of psychologically inspired models of human cognitive function.However,we will use it quite generally to refer to neural networks without reference to any particular field of application. The artificial equivalents of biological neurons are the nodes or units in our preliminary definition and a prototypical example is shown in Figure 12.Synapses are modelled by a single number or weight so that each input is multiplied by a weight before being sent to the equivalent of the cell body.Here,the weighted signals are summed together by simple arithmetic addition to supply a node activation.In the type of node shown in Figure 12-the so-called threshold logic unit (TLU)-the activation is then compared with a threshold;if the activation exceeds the threshold,the unit produces a high-valued output(conventionally"1"), otherwise it outputs zero.In the figure,the size of signals is represented by Weights Threshold Add >0e1 Figure 1.2 Simple artificial neuron. Output layer Inputs 14
It is this architecture and style of processing that we hope to incorporate in neural networks and, because of the emphasis on the importance of the interneuron connections, this type of system is sometimes referred to as being connectionist and the study of this general approach as connectionism. This terminology is often the one encountered for neural networks in the context of psychologically inspired models of human cognitive function. However, we will use it quite generally to refer to neural networks without reference to any particular field of application. The artificial equivalents of biological neurons are the nodes or units in our preliminary definition and a prototypical example is shown in Figure 1.2. Synapses are modelled by a single number or weight so that each input is multiplied by a weight before being sent to the equivalent of the cell body. Here, the weighted signals are summed together by simple arithmetic addition to supply a node activation. In the type of node shown in Figure 1.2—the so-called threshold logic unit (TLU)—the activation is then compared with a threshold; if the activation exceeds the threshold, the unit produces a high-valued output (conventionally "1"), otherwise it outputs zero. In the figure, the size of signals is represented by Figure 1.2 Simple artificial neuron. 14

Figure 1.3 Simple example of neural network. the width of their corresponding arrows,weights are shown by multiplication symbols in circles,and their values are supposed to be proportional to the symbol's size;only positive weights have been used.The TLU is the simplest (and historically the earliest(McCulloch Pitts 1943))model of an artificial neuron. The term "network"will be used to refer to any system of artificial neurons.This may range from something as simple as a single node to a large collection of nodes in which each one is connected to every other node in the net.One type of network is shown in Figure 1.3.Each node is now shown by only a circle but weights are implicit on all connections.The nodes are arranged in a layered structure in which each signal emanates from an input and passes via two nodes before reaching an output beyond which it is no longer transformed.This feedforward structure is only one of several available and is typically used to place an input pattern into one of several classes according to the resulting pattern of outputs.For example,if the input consists of an encoding of the patterns of light and dark in an image of handwritten letters,the output layer(topmost in the figure)may contain 26 nodes- one for each letter of the alphabet-to flag which letter class the input character is from.This would be done by allocating one output node per class and requiring that only one such node fires whenever a pattern of the corresponding class is supplied at the input. So much for the basic structural elements and their operation.Returning to our working definition,notice the emphasis on learning from experience.In real neurons the synaptic strengths may,under certain circumstances,be modified so that the behaviour of each neuron can change or adapt to its particular stimulus input.In artificial neurons the equivalent of this is the modification of the weight values.In terms of processing information,there are no computer programs here-the "knowledge"the network has is supposed to be stored in its weights,which evolve by a process of adaptation to stimulus from a set of pattern examples.In one training paradigm called supervised learning,used in conjunction with nets of the type shown in Figure 13,an input pattern is presented to the net and its response then compared with a target output.In terms of our previous letter recognition example,an "A",say,may be input and the network output compared with the classification code for A.The difference between the two patterns of output then determines how the weights are altered.Each particular recipe for change constitutes a learning rule,details of which form a substantial part of subsequent chapters.When the required weight updates have been made another pattern is presented,the output compared with the target,and new changes made.This sequence of events is repeated iteratively many times until (hopefully)the network's behaviour converges so that its response to each pattern is close to the 15
Figure 1.3 Simple example of neural network. the width of their corresponding arrows, weights are shown by multiplication symbols in circles, and their values are supposed to be proportional to the symbol's size; only positive weights have been used. The TLU is the simplest (and historically the earliest (McCulloch & Pitts 1943)) model of an artificial neuron. The term "network" will be used to refer to any system of artificial neurons. This may range from something as simple as a single node to a large collection of nodes in which each one is connected to every other node in the net. One type of network is shown in Figure 1.3. Each node is now shown by only a circle but weights are implicit on all connections. The nodes are arranged in a layered structure in which each signal emanates from an input and passes via two nodes before reaching an output beyond which it is no longer transformed. This feedforward structure is only one of several available and is typically used to place an input pattern into one of several classes according to the resulting pattern of outputs. For example, if the input consists of an encoding of the patterns of light and dark in an image of handwritten letters, the output layer (topmost in the figure) may contain 26 nodes— one for each letter of the alphabet—to flag which letter class the input character is from. This would be done by allocating one output node per class and requiring that only one such node fires whenever a pattern of the corresponding class is supplied at the input. So much for the basic structural elements and their operation. Returning to our working definition, notice the emphasis on learning from experience. In real neurons the synaptic strengths may, under certain circumstances, be modified so that the behaviour of each neuron can change or adapt to its particular stimulus input. In artificial neurons the equivalent of this is the modification of the weight values. In terms of processing information, there are no computer programs here—the "knowledge" the network has is supposed to be stored in its weights, which evolve by a process of adaptation to stimulus from a set of pattern examples. In one training paradigm called supervised learning, used in conjunction with nets of the type shown in Figure 1.3, an input pattern is presented to the net and its response then compared with a target output. In terms of our previous letter recognition example, an "A", say, may be input and the network output compared with the classification code for A. The difference between the two patterns of output then determines how the weights are altered. Each particular recipe for change constitutes a learning rule, details of which form a substantial part of subsequent chapters. When the required weight updates have been made another pattern is presented, the output compared with the target, and new changes made. This sequence of events is repeated iteratively many times until (hopefully) the network's behaviour converges so that its response to each pattern is close to the 15

corresponding target.The process as a whole,including any ordering of pattern presentation,criteria for terminating the process,etc.,constitutes the training algorithm. What happens if,after training,we present the network with a pattern it hasn't seen before?If the net has learned the underlying structure of the problem domain then it should classify the unseen pattern correctly and the net is said to generalize well.If the net does not have this property it is little more than a classification lookup table for the training set and is of little practical use.Good generalization is therefore one of the key properties of neural networks. 16
corresponding target. The process as a whole, including any ordering of pattern presentation, criteria for terminating the process, etc., constitutes the training algorithm. What happens if, after training, we present the network with a pattern it hasn't seen before? If the net has learned the underlying structure of the problem domain then it should classify the unseen pattern correctly and the net is said to generalize well. If the net does not have this property it is little more than a classification lookup table for the training set and is of little practical use. Good generalization is therefore one of the key properties of neural networks. 16

1.2 Why study neural networks? This question is pertinent here because,depending on one's motive,the study of connectionism can take place from differing perspectives.It also helps to know what questions we are trying to answer in order to avoid the kind of religious wars that sometimes break out when the words "connectionism"or "neural network"are mentioned. Neural networks are often used for statistical analysis and data modelling,in which their role is perceived as an alternative to standard nonlinear regression or cluster analysis techniques (Cheng Titterington 1994).Thus,they are typically used in problems that may be couched in terms of classification,or forecasting.Some examples include image and speech recognition,textual character recognition,and domains of human expertise such as medical diagnosis,geological survey for oil, and financial market indicator prediction.This type of problem also falls within the domain of classical artificial intelligence (AI)so that engineers and computer scientists see neural nets as offering a style of parallel distributed computing, thereby providing an alternative to the conventional algorithmic techniques that have dominated in machine intelligence.This is a theme pursued further in the final chapter but,by way of a brief explanation of this term now,the parallelism refers to the fact that each node is conceived of as operating independently and concurrently (in parallel with)the others,and the "knowledge"in the network is distributed over the entire set of weights,rather than focused in a few memory locations as in a conventional computer.The practitioners in this area do not concern themselves with biological realism and are often motivated by the ease of implementing solutions in digital hardware or the efficiency and accuracy of particular techniques.Haykin(1994)gives a comprehensive survey of many neural network techniques from an engineering perspective. Neuroscientists and psychologists are interested in nets as computational models of the animal brain developed by abstracting what are believed to be those properties of real nervous tissue that are essential for information processing.The artificial neurons that connectionist models use are often extremely simplified versions of their biological counterparts and many neuroscientists are sceptical about the ultimate power of these impoverished models,insisting that more detail is necessary to explain the brain's function.Only time will tell but,by drawing on knowledge about how real neurons are interconnected as local "circuits", substantial inroads have been made in modelling brain functionality.A good introduction to this programme of computational neuroscience is given by Churchland Sejnowski (1992). Finally,physicists and mathematicians are drawn to the study of networks from an 17
1.2 Why study neural networks? This question is pertinent here because, depending on one's motive, the study of connectionism can take place from differing perspectives. It also helps to know what questions we are trying to answer in order to avoid the kind of religious wars that sometimes break out when the words "connectionism" or "neural network" are mentioned. Neural networks are often used for statistical analysis and data modelling, in which their role is perceived as an alternative to standard nonlinear regression or cluster analysis techniques (Cheng & Titterington 1994). Thus, they are typically used in problems that may be couched in terms of classification, or forecasting. Some examples include image and speech recognition, textual character recognition, and domains of human expertise such as medical diagnosis, geological survey for oil, and financial market indicator prediction. This type of problem also falls within the domain of classical artificial intelligence (AI) so that engineers and computer scientists see neural nets as offering a style of parallel distributed computing, thereby providing an alternative to the conventional algorithmic techniques that have dominated in machine intelligence. This is a theme pursued further in the final chapter but, by way of a brief explanation of this term now, the parallelism refers to the fact that each node is conceived of as operating independently and concurrently (in parallel with) the others, and the "knowledge" in the network is distributed over the entire set of weights, rather than focused in a few memory locations as in a conventional computer. The practitioners in this area do not concern themselves with biological realism and are often motivated by the ease of implementing solutions in digital hardware or the efficiency and accuracy of particular techniques. Haykin (1994) gives a comprehensive survey of many neural network techniques from an engineering perspective. Neuroscientists and psychologists are interested in nets as computational models of the animal brain developed by abstracting what are believed to be those properties of real nervous tissue that are essential for information processing. The artificial neurons that connectionist models use are often extremely simplified versions of their biological counterparts and many neuroscientists are sceptical about the ultimate power of these impoverished models, insisting that more detail is necessary to explain the brain's function. Only time will tell but, by drawing on knowledge about how real neurons are interconnected as local "circuits", substantial inroads have been made in modelling brain functionality. A good introduction to this programme of computational neuroscience is given by Churchland & Sejnowski (1992). Finally, physicists and mathematicians are drawn to the study of networks from an 17