
Comparison with DIT-FFT and DFT Digital Signal Processing--DFT/FFT Algorithms each stage computation needs N/2 complex multiplication and N complex addition。SoM stages computations totally need CM(2)= Mlog N N 2 complex addition C4(2)=N·M=Nlog2N DFT/FFT N2 2N (N/2)log2 N 10g2 N eg,N=210=1024 N2 1048576 204.8 (N/2)log,N 5120 上游充通大
Digital Signal Processing—— DFT/FFT Algorithms Comparison with DIT―FFT and DFT each stage computation needs N/2 complex multiplication and N complex addition 。 So M stages computations totally need 2 2 (2) log 2 2 (2) log M A N N C M N C N M N N complex addition eg,N=2 10=1024 2 2 1048576 204.8 ( / 2)log 5120 N N N DFT/FFT 2 2 2 2 ( / 2)log log N N N N N

Comparison with DIT-FFT and DFT Digital Signal Processing--DFT/FFT Algorithms N2 N N2 Nlog N 2 N log,N 2 4 1 4.0 4 16 4 4.0 8 64 12 5.4 16 256 32 8.0 32 1024 80 12.8 64 4096 192 21.4 128 16394 448 36.6 256 65536 1024 64.0 512 262114 2304 113.8 1024 1048576 5120 204.8 2048 4194304 11264 372.4 上泽充通大
Digital Signal Processing—— DFT/FFT Algorithms Comparison with DIT―FFT and DFT N 2 N 2 log 2 N N 2 2 log 2 N N N 2 4 1 4.0 4 16 4 4.0 8 64 12 5.4 16 256 32 8.0 32 1024 80 12.8 64 4096 192 21.4 128 16394 448 36.6 256 65536 1024 64.0 512 262114 2304 113.8 1024 1048576 5120 204.8 2048 4194304 11264 372.4
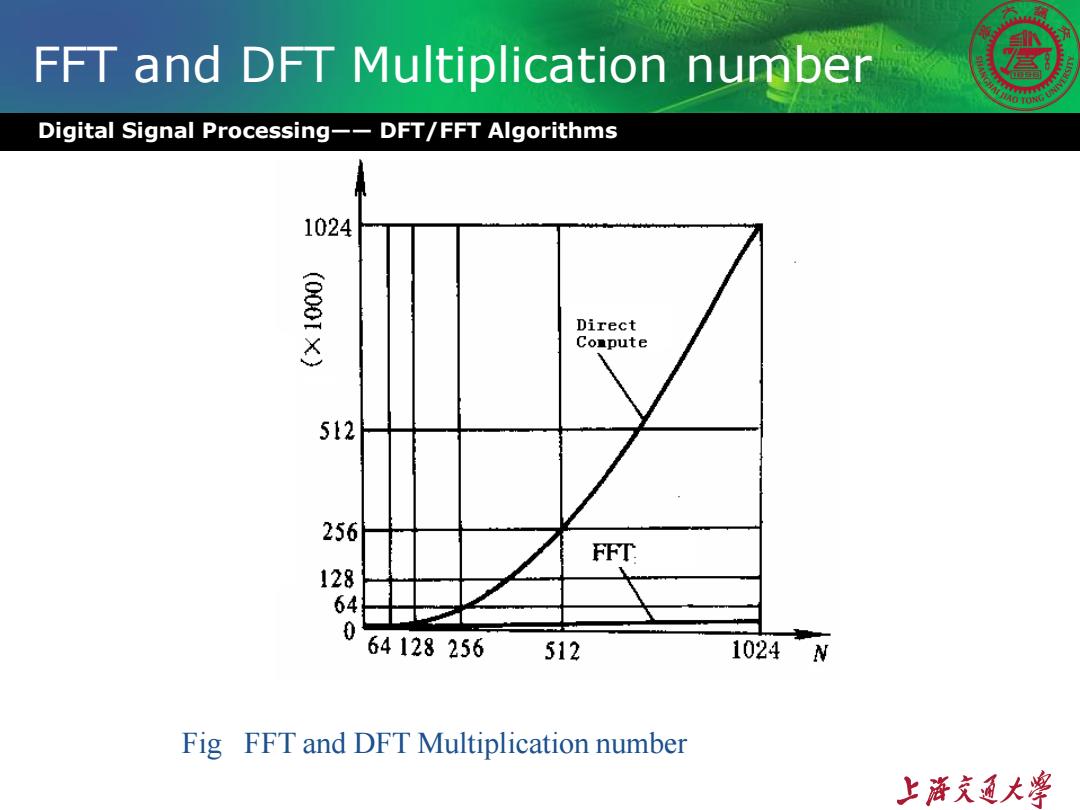
FFT and DFT Multiplication number Digital Signal Processing--DFT/FFT Algorithms 1024 (000tX) Direct Compute 512 256 FFT 128 64128256 512 1024N Fig FFT and DFT Multiplication number 上游充通大¥
Digital Signal Processing—— DFT/FFT Algorithms FFT and DFT Multiplication number Fig FFT and DFT Multiplication number

DIT-FFT Computation Law and Programming Thinking Digital Signal Processing--DFT/FFT Algorithms 1.bit computation DIT-FFT computation procedure is regular. N=2M-point FFT has M stage computation, and each stage has N/2 butterfly computation。 2.Twiddle factor WN Regularity In N-point DIT-FFT computation each stage has N/2 butterfly Each butterfly must multiply WPN,that is twiddle factor,p exponent is of twiddle factor. 上游充通大¥
Digital Signal Processing—— DFT/FFT Algorithms DIT―FFT Computation Law and Programming Thinking 1.bit computation DIT―FFT computation procedure is regular。 N=2M-point FFT has M stage computation, and each stage has N/2 butterfly computation。 2.Twiddle factor WN Regularity In N-point DIT―FFT computation , each stage has N/2 butterfly 。 Each butterfly must multiply Wp N,that is twiddle factor,p exponent is of twiddle factor

DIT-FFT Computation Law and Programming Thinking Digital Signal Processing--DFT/FFT Algorithms L stage has 2 L-1 different twiddle factor When N=23=8,twiddle factor *L=1,WR=WW4=W以,=0 *L=2,WR=W2=W,J=0,1 *L=3,WR=WW=W,J=0,1,2,3 N=2M,L stage twiddle factor: WW=W,J=0,1,2,…,24-1 2=2M×2-M=N.2-M W时=W24w=W2,J=0,12,,2-1-1 p=J.2M-L 上游充通大
Digital Signal Processing—— DFT/FFT Algorithms DIT―FFT Computation Law and Programming Thinking L stage has 2 L-1 different twiddle factor 。When N=23=8, twiddle factor : N=2M ,L stage twiddle factor: 1 2 2 1 2 , 0,1,2, ,2 1 2 2 2 2 , 0,1,2, ,2 1 2 L M L L M p J L N L M L M L M P J J L N N N M L W W J N W W W J p J / 4 2 / 2 2 2 1, , 0 2, , 0,1 3, , 0,1,2,3 L L L p J J N N p J J N N p J J N N L W W W J L W W W J L W W W J