
Basic principle of DIT-FFT Digital Signal Processing--DFT/FFT Algorithms FFT Algorithm has 2 types Decimation In Time FFT,(DIT-FFT) and Decimation In Frequency FFT(DIF-FFT)。First DIF-FFT。 Length of x(n)is N,and N=2M,M∈N Depended on odd-even of n,x(n)is divided into two N/2-point sub-sequence N x(r)=x(2r), r=0,1,.-1 2 x2(r)=x(2r+1),r=0,1,. 上游交通大学
Digital Signal Processing—— DFT/FFT Algorithms Basic principle of DIT-FFT FFT Algorithm has 2 types : Decimation In Time FFT,(DIT-FFT) and Decimation In Frequency FFT(DIF―FFT)。First DIF―FFT。 Length of x(n) is N,and Depended on odd-even of n, x(n) is divided into two N/2-point sub-sequence 2 , M N M ∈N 1 2 ( ) (2 ), 0,1, 1 2 ( ) (2 1), 0,1, 1 2 N x r x r r N x r x r r

DIT-FFT Digital Signal Processing--DFT/FFT Algorithms DFT[X(n)]=X(k)=∑x(n)W+∑x(n)W n= N72 W/2-1 ∑x(2r)w+∑x(2r+1)w2+ r= =0 N/2-1 N/2-1 (rW2+m∑x(r)W r=0 三0 2π JN W 22k 二e JN =e 2 =W2 N/2-1 N/2-1 .X(k)=∑ x(rW+Wx(rW2=X(k)+WX(k) r=0 上游充通大¥
Digital Signal Processing—— DFT/FFT Algorithms DIT-FFT DFT [x(n)]= /2 1 /2 1 2 (2 1) 0 0 /2 1 /2 1 2 2 1 2 0 0 ( ) ( ) ( ) (2 ) (2 1) ( ) ( ) kn kn N N n n N N kr k r N N r r N N kr k kr N N N r r X k x n W x n W x r W x r W x r W W x r W ∵ 2 2 2 2 2 / 2 j kr N j kr kr kr N W e e W N N ∴ / 2 1 / 2 1 1 / 2 2 / 2 1 2 0 0 ( ) ( ) ( ) ( ) ( ) N N kr k kr k N N N N r r X k x r W W x r W X k W X k

DIT-FFT Digital Signal Processing--DFT/FFT Algorithms X1(k)=DFT[x1(r)]X2(k)=DFT[x2(r)]N/2Points, That is N/2-1 X (k)=>x(r)WN2=DFT[x(r)] r=0 /2-1 X,()=∑ x2(r)WNn2=DFT[x2(r)] r=0 X(k)、X,k)(N/2),And m宁=-n,∴Xk) X(k)=X(k)+WX2()k=0,1,. Xk+当=x-WX,)k=0,1 2 上游充通大粤
Digital Signal Processing—— DFT/FFT Algorithms DIT-FFT X1(k)=DFT[x1(r)]、X2(k)=DFT[ x2(r)] N/2Points, That is / 2 1 1 1 / 2 1 0 / 2 1 2 2 / 2 2 0 ( ) ( ) [ ( )] ( ) ( ) [ ( )] N kr N r N kr N r X k x r W DFT x r X k x r W DFT x r X1 (k)、X2 (k) (N/2),And ,∴X(k) 2 N k k W W N N 1 2 1 2 ( ) ( ) ( ) 0,1, 1 2 ( ) ( ) ( ) 0,1, 1 2 2 k N k N N X k X k W X k k N N X k X k W X k k

DIT-FFT Digital Signal Processing--DFT/FFT Algorithms A A十BC B ·A-BC Fig Butterfly computation 上游充通大学
Digital Signal Processing—— DFT/FFT Algorithms DIT-FFT C A B A+ B C A- B C Fig Butterfly computation
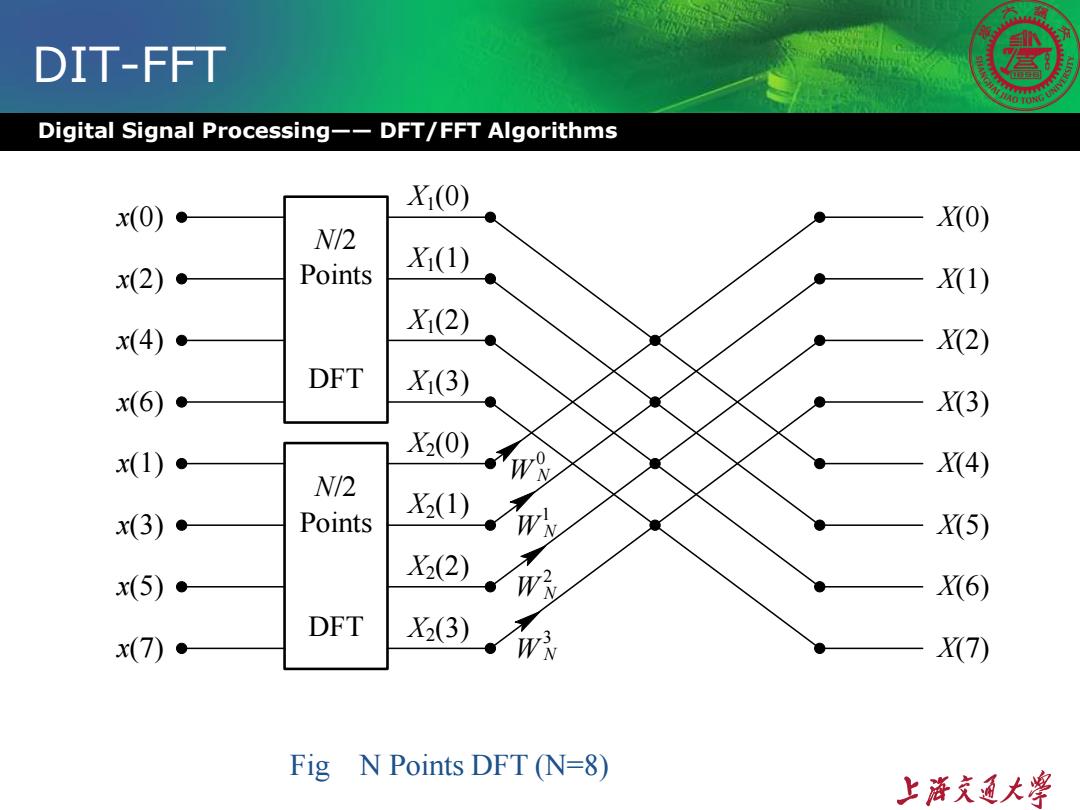
DIT-FFT Digital Signal Processing--DFT/FFT Algorithms X(0) x(0) ● X(0) N/2 Points X1(1) x(2) X1) X1(2) x(4) X2) DFT X(3) x(6) X3) X2(0) x(1) X4) N/2 X2(1) x(3) Points X5) X2(2) x(5) W呢 X6) DFT X2(3) x(7) P究 X7) Fig N Points DFT(N=8) 上游充通大¥
Digital Signal Processing—— DFT/FFT Algorithms DIT-FFT Fig N Points DFT (N=8) N/2 Points DFT W N 0 N/2 Points DFT W N 1 W N 2 W N 3 x(0) X1(0) x(2) x(4) x(6) x(1) x(3) x(5) x(7) X1(1) X1(2) X1(3) X2(0) X2(1) X2(2) X2(3) X(0) X(1) X(2) X(3) X(4) X(5) X(6) X(7)